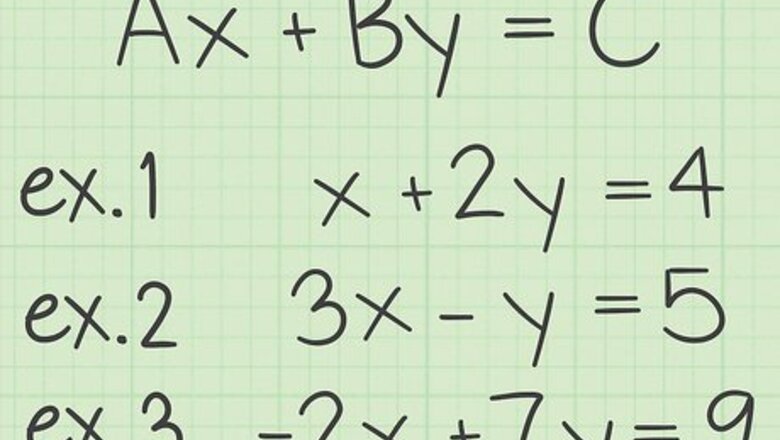
views
Arranging the Equations to Begin Solving
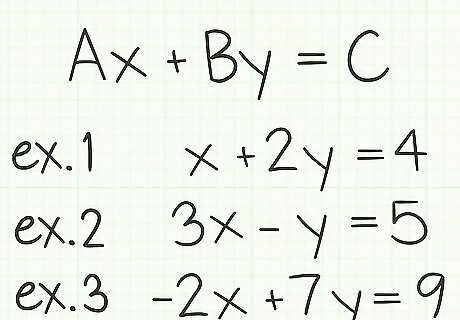
Recognize the standard format. In algebra, the “standard format” for an equation is written as A x + B y = C {\displaystyle Ax+By=C} Ax+By=C. When written in this format, the letters A, B and C are commonly chosen to represent numerical values, while x and y are the variables that you need to solve. You could easily work with different variables, but the structure of the standard format will be the same. For example, if you are solving a business-related problem about selling hats and scarves to calculate the total number of items sold, you might choose the variable h {\displaystyle h} h to represent the number of hats and s {\displaystyle s} s to represent the number of scarves. Your standard format in this case would look like A h + B s = T {\displaystyle Ah+Bs=T} Ah+Bs=T. The steps for solving the problem will still be the same.
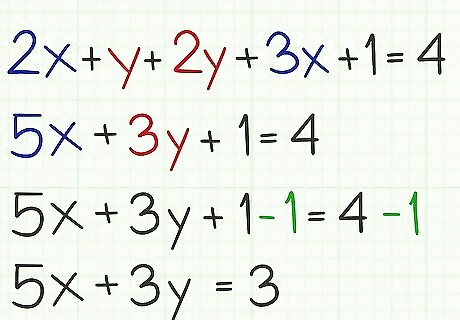
Rearrange your equations to put them into standard format. This may require you to combine similar terms, if each variable appears in the equation more than once, for example. You will also need to move the terms so they appear in the proper order. For example, given the equation 2 x + y + 2 y + 3 x + 1 = 4 {\displaystyle 2x+y+2y+3x+1=4} 2x+y+2y+3x+1=4, you need to perform the following steps to get to standard format: 2 x + y + 2 y + 3 x + 1 = 4 {\displaystyle 2x+y+2y+3x+1=4} 2x+y+2y+3x+1=4 (given equation) 5 x + 3 y + 1 = 4 {\displaystyle 5x+3y+1=4} 5x+3y+1=4 (combine like terms) 5 x + 3 y = 3 {\displaystyle 5x+3y=3} 5x+3y=3 (subtract 1 from both sides) You may be familiar with seeing linear equations in the form y = m x + b {\displaystyle y=mx+b} y=mx+b. This is called the “slope-intercept” form of a line. It is useful for different purposes. It could be used to solve the system by linear combinations, but the standard format Ax+By=C is preferred. If you have your data in the slope-intercept form, you will need to rewrite it algebraically into standard format as follows: y = m x + b {\displaystyle y=mx+b} y=mx+b (given slope-intercept form) y − m x = b {\displaystyle y-mx=b} y-mx=b (subtract mx from both sides) - m x + y = b {\displaystyle mx+y=b} mx+y=b (rearrange terms to get x first) A=-m, B=1, C=b (redefine terms for standard format)
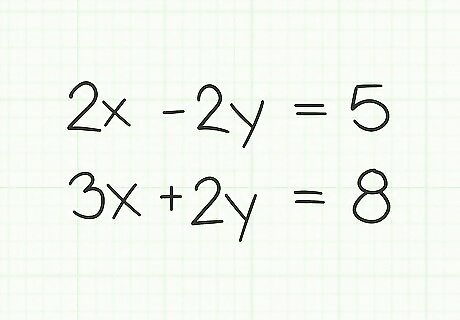
Write your equations so the variables line up. It is helpful to write your equations with one directly over the other, so the similar terms line up. For example, if you have the two equations, in standard format, of 2 x − 2 y = 5 {\displaystyle 2x-2y=5} 2x-2y=5 and 3 x + 2 y = 8 {\displaystyle 3x+2y=8} 3x+2y=8, write them in two rows as: 2 x − 2 y = 5 {\displaystyle 2x-2y=5} 2x-2y=5 3 x + 2 y = 8 {\displaystyle 3x+2y=8} 3x+2y=8
Using Linear Combinations if a Pair of Coefficients Match
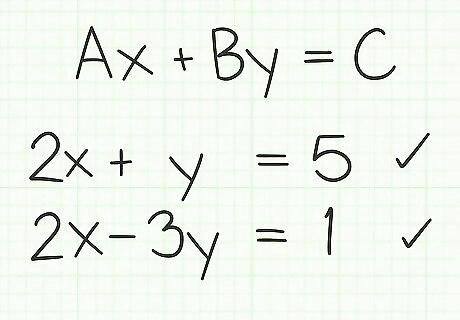
Examine the equations in standard format. When you have your equations written in standard format, lined up so the similar terms are aligned, check the coefficients. You are looking for one pair of coefficients that match. For example, consider these two equations: 2 x + y = 5 {\displaystyle 2x+y=5} 2x+y=5 2 x − 3 y = 1 {\displaystyle 2x-3y=1} 2x-3y=1 You should see very quickly that the term 2 x {\displaystyle 2x} 2x appears identically in each equation. Be very careful when matching the terms. Look for the signs (plus or minus) to match as well. For this method of solving, the terms 2 x {\displaystyle 2x} 2x and − 2 x {\displaystyle -2x} -2x are NOT considered to be the same. If your system does not have a matching pair of coefficients, you cannot use this method for solving. You will need to go on to the next method.
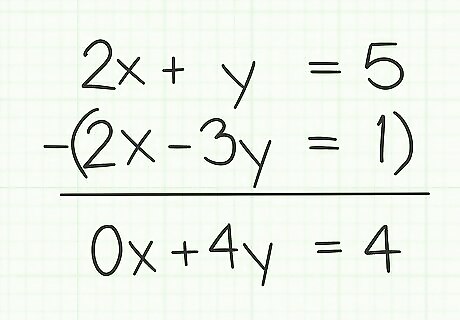
Subtract corresponding terms. Working across the system from left to right, subtract each term of the second equation from the corresponding term of the first equation. It may be helpful simply to draw a long horizontal line across the bottom of the two equations and subtract downward, as you would with any ordinary subtraction problem. 2 x + y = 5 {\displaystyle 2x+y=5} 2x+y=5 2 x − 3 y = 1 {\displaystyle 2x-3y=1} 2x-3y=1 ------------------------ 0 x + 4 y = 4 {\displaystyle 0x+4y=4} 0x+4y=4
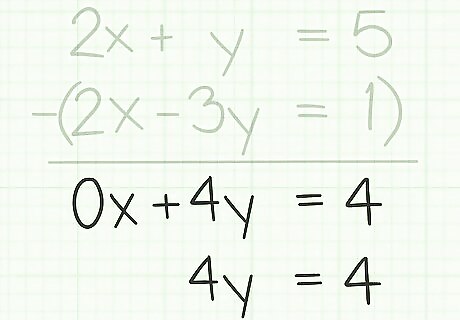
Write out the result. If one of your terms matched exactly, as it should, and you subtracted correctly, then one of the variables should be eliminated from the problem. Rewrite what you have left as a single equation. In the example above, you should be left with 4 y = 4 {\displaystyle 4y=4} 4y=4. Because one of the variables gets eliminated in this method, some textbooks will refer to this as the “elimination” method of solving a system of equations.
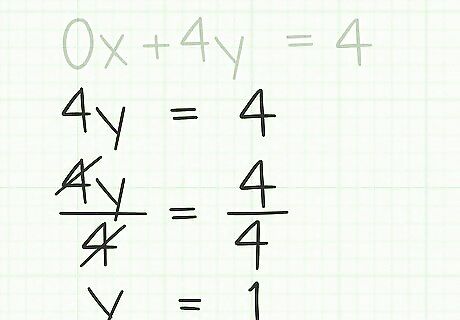
Solve for the remaining variable. What you have left should be a fairly simple, one-variable equation. Solve it by dividing both sides of the equation by the coefficient. In the example above, divide both sides of 4 y = 4 {\displaystyle 4y=4} 4y=4 by 4. You will be left with the solution y = 1 {\displaystyle y=1} y=1.
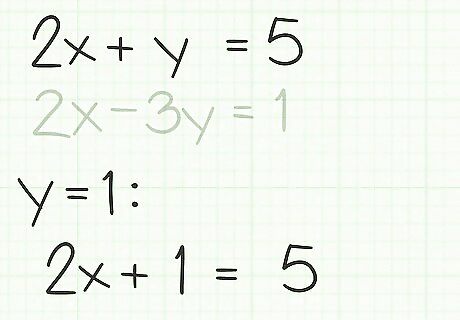
Replace that solution into one of your original equations. Take that solution, in our example y=1, and substitute it in place of y {\displaystyle y} y in either one of the original equations. In this case, we can choose the first example, 2 x + y = 5 {\displaystyle 2x+y=5} 2x+y=5. When you replace the variable with its solution, you will have 2 x + 1 = 5 {\displaystyle 2x+1=5} 2x+1=5.
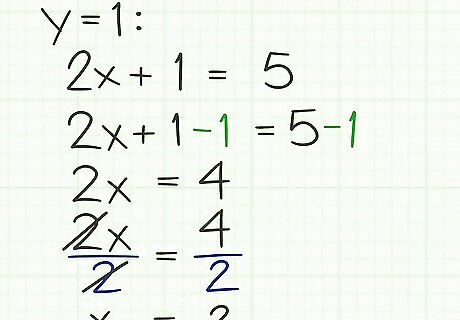
Solve for the remaining variable. Use basic algebraic steps to solve for the remaining variable. Remember that whatever action you do to one side of the equation, you must also do to the other side. For example: 2 x + 1 = 5 {\displaystyle 2x+1=5} 2x+1=5 (original equation) 2 x = 4 {\displaystyle 2x=4} 2x=4 (subtract 1 from both sides) x = 2 {\displaystyle x=2} x=2 (divide both sides by 2 to get solution)
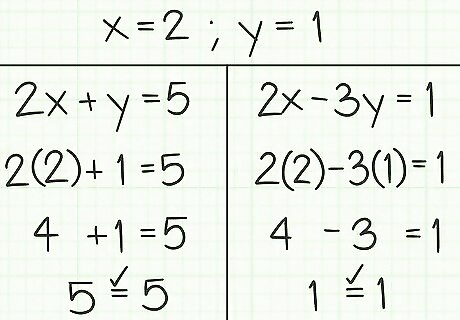
Check your two solutions. Verify that you have done the work correctly by checking your solutions. You should be able to place your two solutions, in this example x = 2 {\displaystyle x=2} x=2 and y = 1 {\displaystyle y=1} y=1, into each of the original equations. When you then simplify the equations, you will get true statements. For example, check the first equation as follows: 2 x + y = 5 {\displaystyle 2x+y=5} 2x+y=5 (original equation) 2 ∗ 2 + 1 = 5 {\displaystyle 2*2+1=5} 2*2+1=5 (insert values for x and y) 4 + 1 = 5 {\displaystyle 4+1=5} 4+1=5 (simplify multiplication) 5 = 5 {\displaystyle 5=5} 5=5 (simplify addition, to get solution) The true statement 5=5 shows the solution is correct. Check the second equation as follows: 2 x − 3 y = 1 {\displaystyle 2x-3y=1} 2x-3y=1 (original equation) 2 ∗ 2 − 3 ∗ 1 = 1 {\displaystyle 2*2-3*1=1} 2*2-3*1=1 (insert values for x and y) 4 − 3 = 1 {\displaystyle 4-3=1} 4-3=1 (simplify multiplication) 1 = 1 {\displaystyle 1=1} 1=1 (simplify subtraction, to get solution) The true statement 1=1 shows the solution is correct.
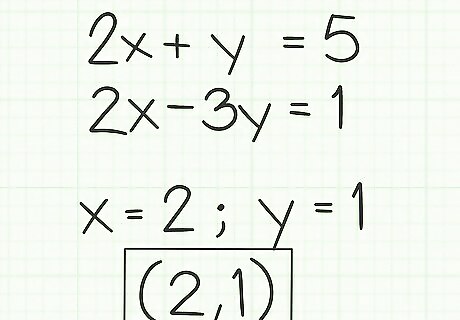
Write out your solution. The final solution, which you have proven to work in both equations, is x = 2 {\displaystyle x=2} x=2 and y = 1 {\displaystyle y=1} y=1. If you are working on graphing linear functions, you may also write your solution as an ordered pair. Thus, for this example, you would write x = 2 {\displaystyle x=2} x=2 and y = 1 {\displaystyle y=1} y=1 in the form ( 2 , 1 ) {\displaystyle (2,1)} (2,1).
Using Linear Combinations if a Pair of Coefficients are Opposites
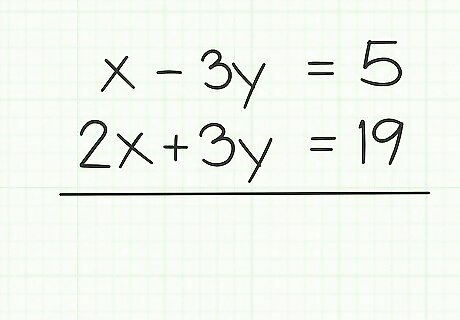
Examine the equations in standard format. Set up your two equations in standard format and look at the coefficients of each of your variables. You are looking for the circumstance where the numbers are the same but the signs are different. Consider this example: x − 3 y = 5 {\displaystyle x-3y=5} x-3y=5 2 x + 3 y = 19 {\displaystyle 2x+3y=19} 2x+3y=19 By examination, you should see that the first equation contains the term − 3 y {\displaystyle -3y} -3y, while the second equation contains the term 3 y {\displaystyle 3y} 3y. These two terms are opposites of each other.
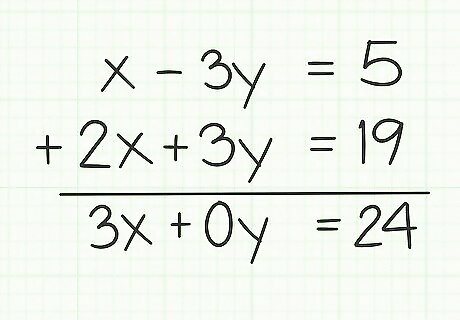
Add corresponding terms. Working across the system from left to right, add each term of the first equation to the corresponding term of the second equation. It may be helpful simply to draw a long horizontal line across the bottom of the two equations and add downward, as you would with any ordinary addition problem. The above example works out as follows: x − 3 y = 5 {\displaystyle x-3y=5} x-3y=5 2 x + 3 y = 19 {\displaystyle 2x+3y=19} 2x+3y=19 ------------------------- 3 x = 24 {\displaystyle 3x=24} 3x=24
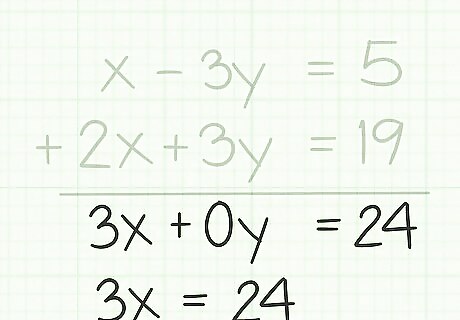
Write out the result. Because you were adding, and one of your terms contained opposites, then one of the variables should be eliminated from the problem. Rewrite what you have left as a single equation. In the example above, the y {\displaystyle y} y variable was eliminated. The remaining equation is 3 x = 24 {\displaystyle 3x=24} 3x=24. Because one of the variables gets eliminated in this method, as with the prior subtraction method, some textbooks will refer to this as the “elimination” method of solving a system of equations.
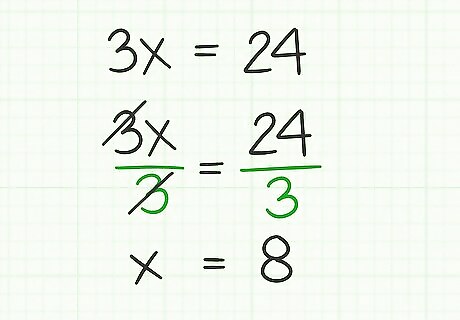
Solve for the remaining variable. What you have left should be a fairly simple, one-variable equation. Solve it by dividing both sides of the equation by the coefficient. In the example above, divide both sides of 3 x = 24 {\displaystyle 3x=24} 3x=24 by 3. You will be left with the solution x = 8 {\displaystyle x=8} x=8.
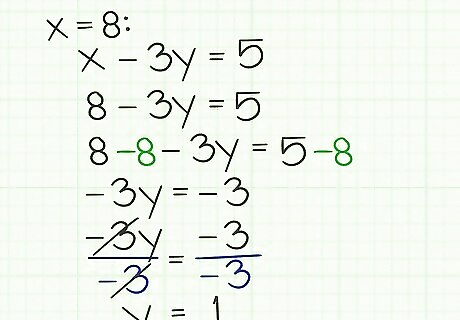
Solve the second variable. Take that solution, in our example x=8, and substitute it in place of
x
{\displaystyle x}
x in either one of the original equations.
Choose the first equation:
x
−
3
y
=
5
{\displaystyle x-3y=5}
x-3y=5 (original equation)
8
−
3
y
=
5
{\displaystyle 8-3y=5}
8-3y=5 (insert value of x)
-
3
y
=
{\displaystyle 3y=}
3y=-
3
{\displaystyle 3}
3 Check your two solutions. Verify that you have done the work correctly by checking your solutions. You should be able to place your two solutions, in this example
x
=
8
{\displaystyle x=8}
x=8 and
y
=
1
{\displaystyle y=1}
y=1, into each of the original equations. When you then simplify the equations, you will get true statements.
For example, start with the first equation:
x
−
3
y
=
5
{\displaystyle x-3y=5}
x-3y=5 (original equation)
8
−
3
∗
1
=
5
{\displaystyle 8-3*1=5}
8-3*1=5 (insert values of x and y)
8
−
3
=
5
{\displaystyle 8-3=5}
8-3=5 (simplify multiplication)
5
=
5
{\displaystyle 5=5}
5=5 (simplify subtraction to get solution)
The true statement 5=5 shows that the solution is correct.
Now try the second equation:
2
x
+
3
y
=
19
{\displaystyle 2x+3y=19}
2x+3y=19 (original equation)
2
∗
8
+
3
∗
1
=
19
{\displaystyle 2*8+3*1=19}
2*8+3*1=19 (insert values of x and y)
16
+
3
=
19
{\displaystyle 16+3=19}
16+3=19 (simplify multiplication)
19
=
19
{\displaystyle 19=19}
19=19 (simplify addition to get solution)
The true statement 19=19 shows that the solution is correct. Write out your solution. The final solution, which you have proven to work in both equations, is
x
=
8
{\displaystyle x=8}
x=8 and
y
=
1
{\displaystyle y=1}
y=1.
If you are working on graphing linear functions, you may also write your solution as an ordered pair. This for this example, you would write
x
=
8
{\displaystyle x=8}
x=8 and
y
=
1
{\displaystyle y=1}
y=1 in the form
(
8
,
1
)
{\displaystyle (8,1)}
(8,1). Examine the equations in standard format. It is more likely that your system of equations will not have a pair of matching or opposite coefficients. When you line up the two equations and compare coefficients, unless two coefficients (the A and B of the standard format) match exactly, you need to take a couple extra steps.
For example, consider these two initial equations:
3
x
+
2
y
=
6
{\displaystyle 3x+2y=6}
3x+2y=6
8
x
−
4
y
=
2
{\displaystyle 8x-4y=2}
8x-4y=2
When you examine them, there are no matching coefficients for similar terms. That is, the 3x does not match the 8x, and the 2y does not match the -4y. There is also no pair of opposites. Create a pair of matching or opposite coefficients. Examine the two equations and decide what number you could use to multiply one of the equations, to create a pair of matching or opposite coefficients. For example, given the system
3
x
+
2
y
=
6
{\displaystyle 3x+2y=6}
3x+2y=6 and
8
x
−
4
y
=
2
{\displaystyle 8x-4y=2}
8x-4y=2, you should be able to see that the first equation contains a term
2
y
{\displaystyle 2y}
2y and the second equation contains a term -
4
y
{\displaystyle 4y}
4y. If you double the first term, you will have a pair of opposite coefficients.
Multiply each term of the equation to create a new equation for solving. In this example, multiply each term of the first equation by
2
{\displaystyle 2}
{\displaystyle 2}. This will turn the original equation
3
x
+
2
y
=
6
{\displaystyle 3x+2y=6}
3x+2y=6 into
6
x
+
4
y
=
12
{\displaystyle 6x+4y=12}
6x+4y=12. Notice that you now have a pair of opposite coefficients in the
y
{\displaystyle y}
y terms of
4
y
{\displaystyle 4y}
4y and -
4
y
{\displaystyle 4y}
4y.
In some cases, you may need to do a double multiplication, or use a fraction. For example, in the system
2
x
−
3
y
=
2
{\displaystyle 2x-3y=2}
2x-3y=2 and
5
x
+
2
y
=
1
{\displaystyle 5x+2y=1}
5x+2y=1, there are no coefficients that are simple integer multiples of each other. You could multiply the first equation by
5
/
2
{\displaystyle 5/2}
5/2 to create
5
x
−
15
2
y
=
5
{\displaystyle 5x-{\frac {15}{2}}y=5}
5x-{\frac {15}{2}}y=5, and now the
x
{\displaystyle x}
x coefficients are ready to be canceled. Alternatively, if you prefer not to work with fractions, you could multiply the first equation by 5 and the second equation by 2. This would create two completely new equations, as follows:
2
x
−
3
y
=
2
{\displaystyle 2x-3y=2}
2x-3y=2 (first original equation)
5
x
+
2
y
=
1
{\displaystyle 5x+2y=1}
5x+2y=1 (second original equation)
Now multiply the first equation by 5, and the second equation by 2
5
∗
(
2
x
−
3
y
=
2
)
{\displaystyle 5*(2x-3y=2)}
5*(2x-3y=2)→→
10
x
−
15
y
=
10
{\displaystyle 10x-15y=10}
10x-15y=10
2
∗
(
5
x
+
2
y
=
1
)
{\displaystyle 2*(5x+2y=1)}
2*(5x+2y=1)→→
10
x
+
4
y
=
2
{\displaystyle 10x+4y=2}
10x+4y=2 Either add or subtract the two new equations. If you have created a matching pair of coefficients, you will subtract terms to eliminate one variable. If you have created a pair of opposite coefficients, you will add terms to eliminate one variable. Consider the following example:
6
x
+
4
y
=
12
{\displaystyle 6x+4y=12}
6x+4y=12 (first equation)
8
x
−
4
y
=
2
{\displaystyle 8x-4y=2}
8x-4y=2 (second equation)
----------------------
14
x
=
14
{\displaystyle 14x=14}
14x=14 (add two equations together to cancel y terms)
x
=
1
{\displaystyle x=1}
x=1 (divide by 14 to get solution) Replace that solution into one of your original equations. Take that solution, in our example x=1, and substitute it in place of
x
{\displaystyle x}
x in either one of the original equations. This works as follows:
3
x
+
2
y
=
6
{\displaystyle 3x+2y=6}
3x+2y=6 (original equation)
3
∗
1
+
2
y
=
6
{\displaystyle 3*1+2y=6}
3*1+2y=6 (insert x value)
3
+
2
y
=
6
{\displaystyle 3+2y=6}
3+2y=6 (simplify multiplication)
2
y
=
3
{\displaystyle 2y=3}
2y=3 (subtract 3 from both sides)
y
=
3
2
{\displaystyle y={\frac {3}{2}}}
y={\frac {3}{2}} (divide both sides by 2) Check your two solutions. Verify that you have done the work correctly by checking your solutions. You should be able to place your two solutions, in this example
x
=
1
{\displaystyle x=1}
x=1 and
y
=
3
2
{\displaystyle y={\frac {3}{2}}}
y={\frac {3}{2}}, into each of the original equations. When you then simplify the equations, you should get true statements.
For example, check the first equation:
3
x
+
2
y
=
6
{\displaystyle 3x+2y=6}
3x+2y=6 (original equation)
3
∗
1
+
2
∗
3
2
=
6
{\displaystyle 3*1+2*{\frac {3}{2}}=6}
3*1+2*{\frac {3}{2}}=6 (insert x and y values)
3
+
3
=
6
{\displaystyle 3+3=6}
3+3=6 (simplify multiplication)
6
=
6
{\displaystyle 6=6}
6=6 (simplify addition to get solution)
The true statement
6
=
6
{\displaystyle 6=6}
6=6 shows that the solution is correct.
Now check the second equation, as follows:
8
x
−
4
y
=
2
{\displaystyle 8x-4y=2}
8x-4y=2 (original equation)
8
∗
1
−
4
∗
3
2
=
2
{\displaystyle 8*1-4*{\frac {3}{2}}=2}
8*1-4*{\frac {3}{2}}=2 (insert x and y values)
8
−
6
=
2
{\displaystyle 8-6=2}
8-6=2 (simplify multiplication)
2
=
2
{\displaystyle 2=2}
2=2 (simplify subtraction)
The true statement
2
=
2
{\displaystyle 2=2}
2=2 shows that the solution is correct. Write out your solution. The final solution, which you have proven to work in both equations, is
x
=
1
{\displaystyle x=1}
x=1 and
y
=
3
2
{\displaystyle y={\frac {3}{2}}}
y={\frac {3}{2}}.
If you are working on graphing linear functions, you may also write your solution as an ordered pair. This for this example, you would write
x
=
1
{\displaystyle x=1}
x=1 and
y
=
3
2
{\displaystyle y={\frac {3}{2}}}
y={\frac {3}{2}} in the form
(
1
,
3
2
)
{\displaystyle (1,{\frac {3}{2}})}
(1,{\frac {3}{2}}). Recognize identical equations as having infinite solutions. In some circumstances, your system of linear equations may have infinite solutions. This means that any pair of values that you insert into the two variables will make the two equations correct. This happens when the two equations are really just algebraic variations of the same, single equation.
For example, consider these two equations:
2
x
+
8
y
=
18
{\displaystyle 2x+8y=18}
2x+8y=18
x
+
4
y
=
9
{\displaystyle x+4y=9}
x+4y=9
If you begin working on this system and try creating a pair of matching coefficients, you will find that by multiplying the second equation by 2 you will create the equation
2
x
+
8
y
=
18
{\displaystyle 2x+8y=18}
2x+8y=18. This is an exact match of the first equation. If you proceed through the steps, you will eventually get the result
0
=
0
{\displaystyle 0=0}
0=0.
A solution of 0=0 means that you have “infinite” solutions or you can simply say that the two equations are identical.
If you consider this system graphically and plot the lines that are represented by the two equations, the “infinite” solution means that the two lines lie exactly one on top of the other. It is really only one line. Find systems with no solution. Occasionally you may have a system in which the two equations, when written in standard form, are nearly identical except that the constant term C is different. Such a system has no solution.
Consider these equations:
4
x
+
2
y
=
6
{\displaystyle 4x+2y=6}
4x+2y=6
2
x
+
y
=
4
{\displaystyle 2x+y=4}
2x+y=4
At first glance, these look like very different equations. However, when you begin solving and multiply each term of the second equation by 2 to try to create matching coefficients, you will wind up with the two equations:
4
x
+
2
y
=
6
{\displaystyle 4x+2y=6}
4x+2y=6
4
x
+
2
y
=
8
{\displaystyle 4x+2y=8}
4x+2y=8
This is an impossible situation, since the expression
4
x
+
2
y
{\displaystyle 4x+2y}
4x+2y cannot equal both 6 and 8 at the same time. If you were to try solving this by subtracting the terms, you would reach the result
0
=
−
2
{\displaystyle 0=-2}
0=-2, which is an incorrect statement. In such a circumstance, your response is that there is no solution to this system.
If you consider what this system means graphically, these are two parallel lines. They will never intersect, so there is no single solution to the system. Use a matrix for systems with more than two variables. It is possible for a system of linear equations to have more than two variables. You may have 3, 4, or as many variables as the problem dictates. Finding a solution to the system means finding a single value for each variable that makes each equation in the system correct. To find a single, unique solution, you must have as many equations as you have variables. Thus, if you have the variables
x
,
y
{\displaystyle x,y}
x,y and
z
{\displaystyle z}
z, you need three equations.
Solving a system of three or more variables can be done using the linear combinations explained here, but that gets very complicated. The preferred method is using matrices, which is too advanced for this article. You may wish to read Use a Graphing Calculator to Solve a System of Equations.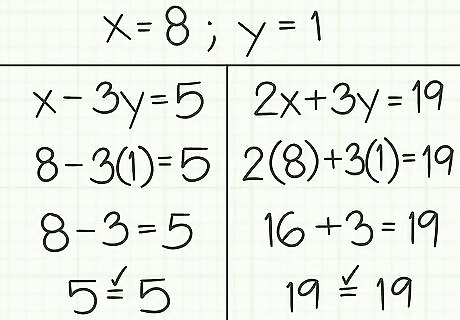
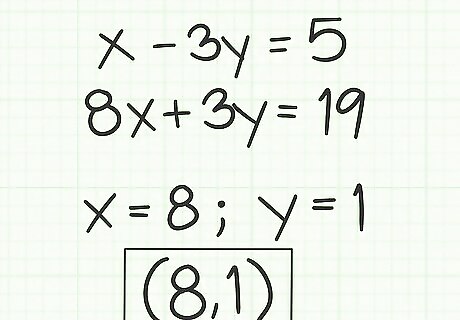
Using Linear Combinations for any Coefficients
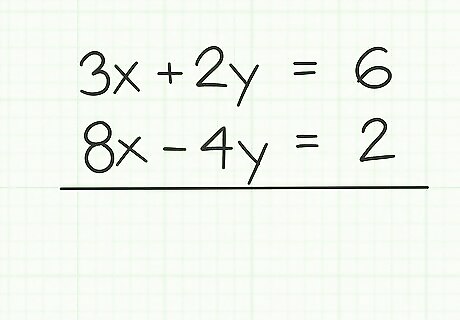
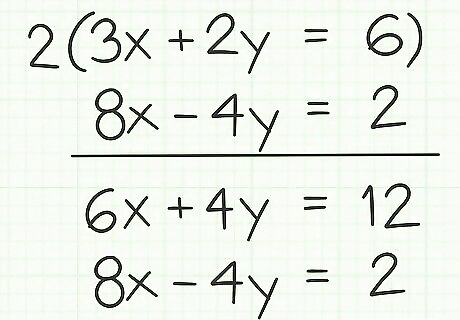
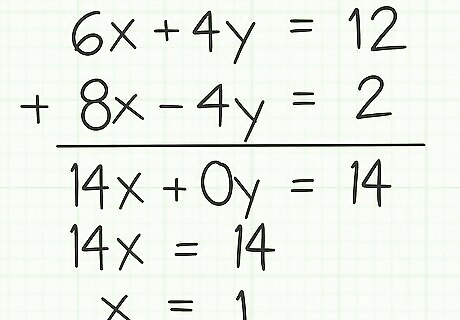
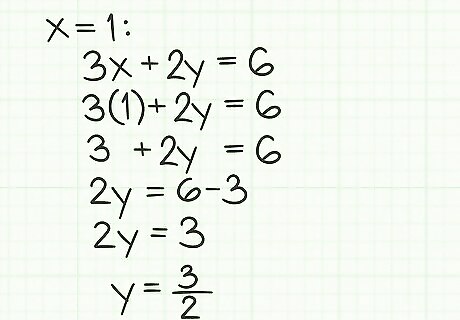
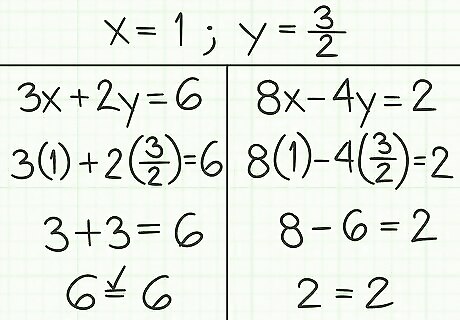
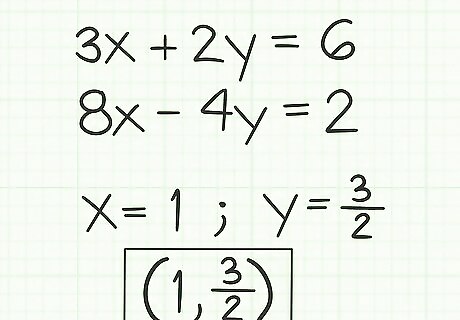
Dealing with Special Circumstances
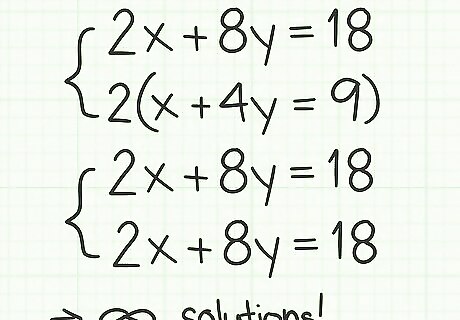
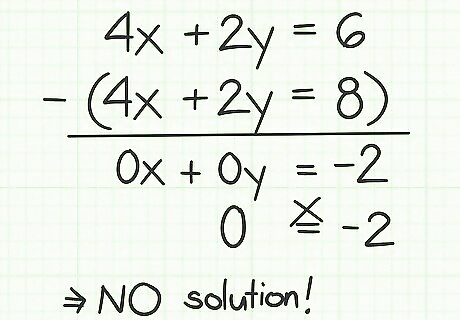
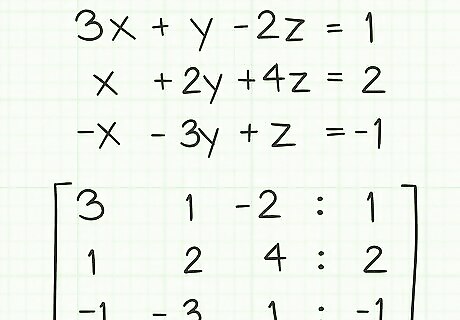

















Comments
0 comment