views
Programming the Formula
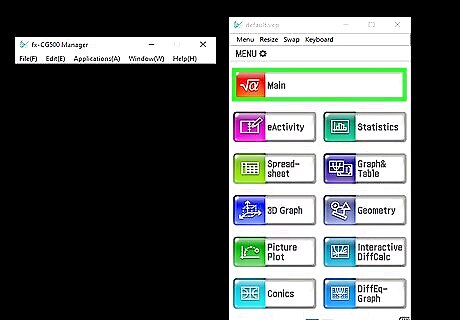
Turn your calculator on and go to the "PRGM" on the menu screen. You can also push "9".
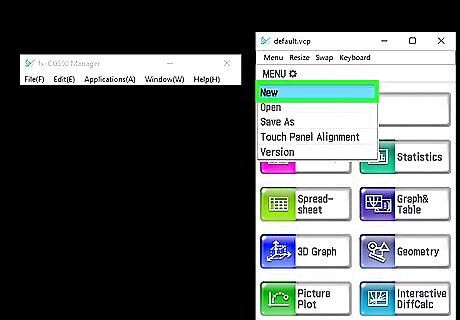
Create a new program by pushing the "F3" button under "NEW".
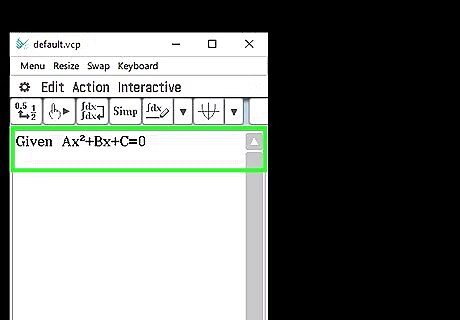
Type in the following: "Given Ax²+Bx+C=0" Push Enter. A small arrow should pop up and you will be on a new line.
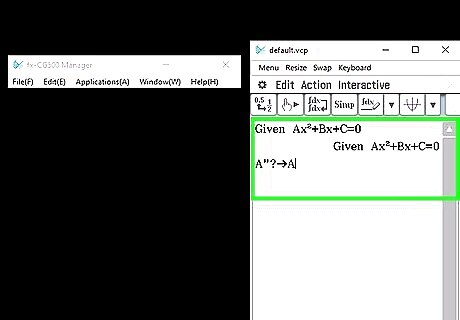
Type the following: "A"?→A In order to get the question mark, push the yellow "SHIFT" button then the "VARS" button. This will actually take you to "PRGM". Push "F4" under "?" to type a "?" To type an arrow, push the arrow button on your calculator. It is just above the "AC/ON" button. Push Enter.
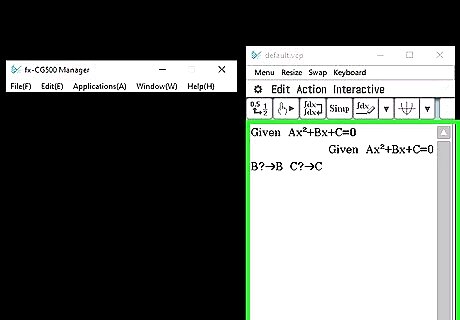
Repeat the previous step, except use "B" and "C". "B"?→B "C"?→C
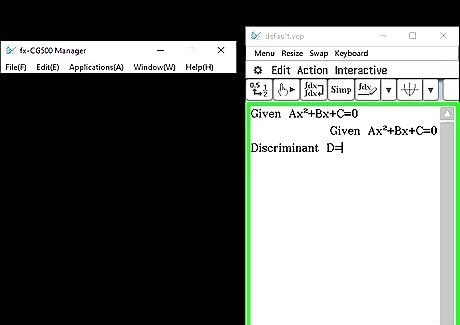
On a new line, type the following: "Discriminant D=" Push Enter
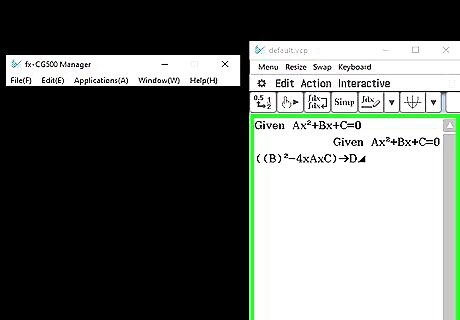
Type the following: ((B)²-4xAxC)→D◢ To get the "◢" symbol, push "SHIFT" then "VARS", and then "F5" under the symbol. Push Enter
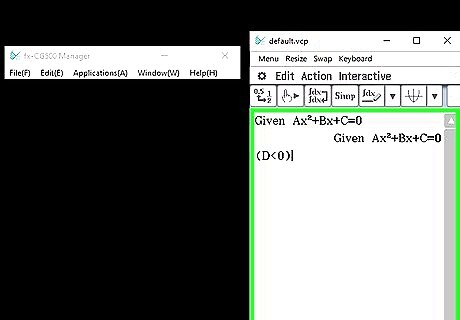
Write the If statement. To get the statements, push "SHIFT", "VARS", then "F1" underneath "COM". If (D<0) Push Enter Then "D<0. No real roots. Imaginary roots:" Enter
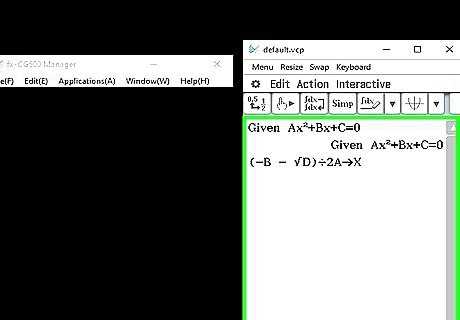
Continue writing: (-B - √D)÷2A→X Enter (-B + √D)÷2A→Y Enter X◢ Enter Y◢ Enter
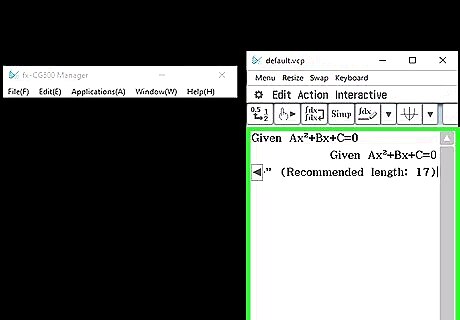
Type the exit message: "-----------------" (Recommended length: 17) Enter "Hit enter to exit." Enter
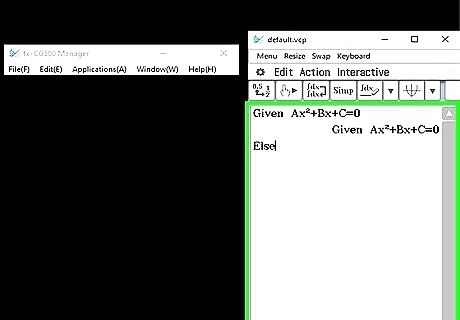
Continue writing. Make sure to use the "Else" from the "COM" section mentioned earlier. Else Enter "Two roots are:" Enter (-B - √D)÷2A→X Enter (-B + √D)÷2A→Y Enter X◢ Enter Y◢ Enter
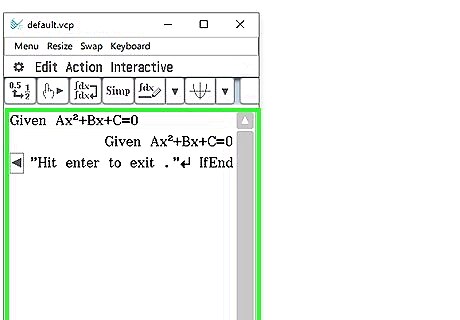
Finish it off: "-----------------" Enter "Hit enter to exit." Enter IfEnd
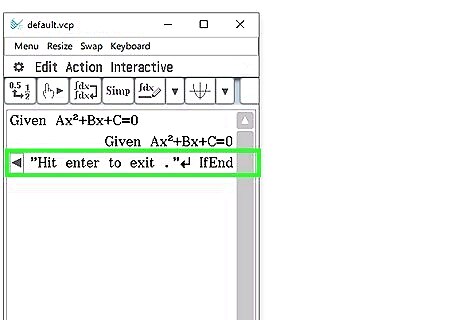
Your code should look like this: "Given Ax²+Bx+C=0"↵ "A"?→A↵ "B"?→B↵ "C"?→C↵ "Discriminant D="↵ ((B)² - 4AC)→D◢ ↵ If (D<0)↵ Then "D<0. No real roots. Imaginary roots:"↵ (-B - √D)÷2A→X↵ (-B + √D)÷2A→Y↵ X◢ ↵ Y◢ "-----------------"↵ "Hit enter to exit ."↵ Else ↵ "Two roots are:"↵ (-B - √D)÷2A→X↵ (-B + √D)÷2A→Y↵ X◢ ↵ Y◢ "-----------------"↵ "Hit enter to exit ."↵ IfEnd
Using the Program
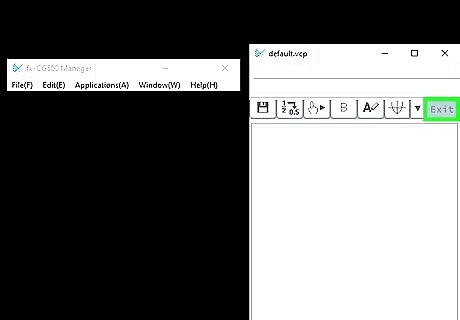
When you finish your program, push "EXIT" to leave the coding area. Then, push "F1" or "EXE" to run the program. The screen should show the following: Given Ax²+Bx+C=0 A? ~Input a value for A and push enter. Repeat for B and C
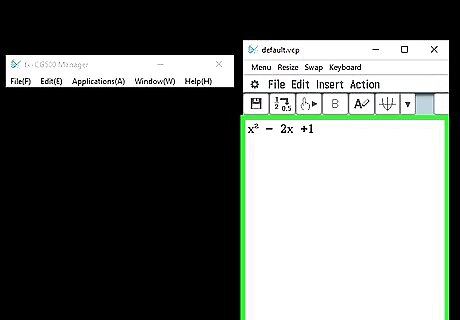
Try testing out some equations: x² - 2x +1 x² - 4 (In this case, b is 0) 4x² + 12x + 5
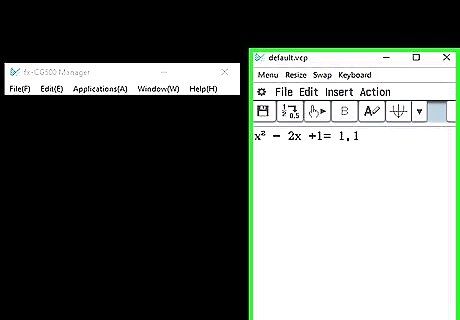
Check your answers. You should get the following answers, respectively: 1, 1 -2, 2 -2.5, -0.5
















Comments
0 comment