How to Tell if a Function Is Even or Odd

Testing the Function Algebraically

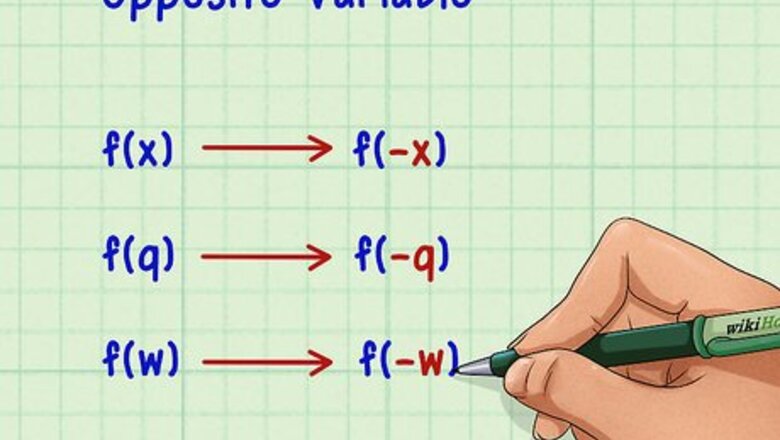
Review opposite variables. In algebra, the opposite of a variable is written as a negative. This is true whether the variable in the function is x {\displaystyle x} x or anything else. If the variable in the original function already appears as a negative (or a subtraction), then its opposite will be a positive (or addition). The following are examples of some variables and their opposites: the opposite of x {\displaystyle x} x is − x {\displaystyle -x} -x the opposite of q {\displaystyle q} q is − q {\displaystyle -q} -q the opposite of − w {\displaystyle -w} -w is w {\displaystyle w} w.

Replace each variable in the function with its opposite. Do not alter the original function other than the sign of the variable. For example: f ( x ) = 4 x 2 − 7 {\displaystyle f(x)=4x^{2}-7} f(x)=4x^{2}-7 becomes f ( − x ) = 4 ( − x ) 2 − 7 {\displaystyle f(-x)=4(-x)^{2}-7} f(-x)=4(-x)^{2}-7 g ( x ) = 5 x 5 − 2 x {\displaystyle g(x)=5x^{5}-2x} g(x)=5x^{5}-2x becomes g ( − x ) = 5 ( − x ) 5 − 2 ( − x ) {\displaystyle g(-x)=5(-x)^{5}-2(-x)} g(-x)=5(-x)^{5}-2(-x) h ( x ) = 7 x 2 + 5 x + 3 {\displaystyle h(x)=7x^{2}+5x+3} h(x)=7x^{2}+5x+3 becomes h ( − x ) = 7 ( − x ) 2 + 5 ( − x ) + 3 {\displaystyle h(-x)=7(-x)^{2}+5(-x)+3} h(-x)=7(-x)^{2}+5(-x)+3.

Simplify the new function. At this stage, you are not concerned with solving the function for any particular numerical value. You simply want to simplify the variables to compare the new function, f(-x), with the original function, f(x). Remember the basic rules of exponents which say that a negative base raised to an even power will be positive, while a negative base raised to an odd power will be negative. f ( − x ) = 4 ( − x ) 2 − 7 {\displaystyle f(-x)=4(-x)^{2}-7} f(-x)=4(-x)^{2}-7 f ( − x ) = 4 x 2 − 7 {\displaystyle f(-x)=4x^{2}-7} f(-x)=4x^{2}-7 g ( − x ) = 5 ( − x ) 5 − 2 ( − x ) {\displaystyle g(-x)=5(-x)^{5}-2(-x)} g(-x)=5(-x)^{5}-2(-x) g ( − x ) = 5 ( − x 5 ) + 2 x {\displaystyle g(-x)=5(-x^{5})+2x} g(-x)=5(-x^{5})+2x g ( − x ) = − 5 x 5 + 2 x {\displaystyle g(-x)=-5x^{5}+2x} g(-x)=-5x^{5}+2x h ( − x ) = 7 ( − x ) 2 + 5 ( − x ) + 3 {\displaystyle h(-x)=7(-x)^{2}+5(-x)+3} h(-x)=7(-x)^{2}+5(-x)+3 h ( − x ) = 7 x 2 − 5 x + 3 {\displaystyle h(-x)=7x^{2}-5x+3} h(-x)=7x^{2}-5x+3

Compare the two functions. For each example that you are testing, compare the simplified version of f(-x) with the original f(x). Line up the terms with each other for easy comparison, and compare the signs of all terms. If the two results are the same, then f(x)=f(-x), and the original function is even. An example is: f ( x ) = 4 x 2 − 7 {\displaystyle f(x)=4x^{2}-7} f(x)=4x^{2}-7 and f ( − x ) = 4 x 2 − 7 {\displaystyle f(-x)=4x^{2}-7} f(-x)=4x^{2}-7. These two are the same, so the function is even. If each term in the new version of the function is the opposite of the corresponding term of the original, then f(x)=-f(-x), and the function is odd. For example: g ( x ) = 5 x 5 − 2 x {\displaystyle g(x)=5x^{5}-2x} g(x)=5x^{5}-2x but g ( − x ) = − 5 x 5 + 2 x {\displaystyle g(-x)=-5x^{5}+2x} g(-x)=-5x^{5}+2x. Notice that if you multiply each term of the first function by -1, you will create the second function. Thus, the original function g(x) is odd. If the new function does not meet either of these two examples, then it is neither even nor odd. For example: h ( x ) = 7 x 2 + 5 x + 3 {\displaystyle h(x)=7x^{2}+5x+3} h(x)=7x^{2}+5x+3 but h ( − x ) = 7 x 2 − 5 x + 3 {\displaystyle h(-x)=7x^{2}-5x+3} h(-x)=7x^{2}-5x+3. The first term is the same in each function, but the second term is an opposite. Therefore, this function is neither even nor odd.

Testing the Function Graphically

Graph the function. Using graph paper or a graphing calculator, draw the graph of the function. Choose several numerical values for x {\displaystyle x} x and insert them into the function to calculate the resulting y {\displaystyle y} y value. Plot these points on the graph and, after you have plotted several points, connect them to see the graph of the function. When plotting points, check positive and corresponding negative values for x {\displaystyle x} x. For example, if working with the function f ( x ) = 2 x 2 + 1 {\displaystyle f(x)=2x^{2}+1} f(x)=2x^{2}+1, plot the following values: f ( 1 ) = 2 ( 1 ) 2 + 1 = 2 + 1 = 3 {\displaystyle f(1)=2(1)^{2}+1=2+1=3} f(1)=2(1)^{2}+1=2+1=3. This gives the point ( 1 , 3 ) {\displaystyle (1,3)} (1,3). f ( 2 ) = 2 ( 2 ) 2 + 1 = 2 ( 4 ) + 1 = 8 + 1 = 9 {\displaystyle f(2)=2(2)^{2}+1=2(4)+1=8+1=9} f(2)=2(2)^{2}+1=2(4)+1=8+1=9. This gives the point ( 2 , 9 ) {\displaystyle (2,9)} (2,9). f ( − 1 ) = 2 ( − 1 ) 2 + 1 = 2 + 1 = 3 {\displaystyle f(-1)=2(-1)^{2}+1=2+1=3} f(-1)=2(-1)^{2}+1=2+1=3. This gives the point ( − 1 , 3 ) {\displaystyle (-1,3)} (-1,3). f ( − 2 ) = 2 ( − 2 ) 2 + 1 = 2 ( 4 ) + 1 = 8 + 1 = 9 {\displaystyle f(-2)=2(-2)^{2}+1=2(4)+1=8+1=9} f(-2)=2(-2)^{2}+1=2(4)+1=8+1=9. This gives the point ( − 2 , 9 ) {\displaystyle (-2,9)} (-2,9).

Test for symmetry across the y-axis. When looking at a function, symmetry suggests a mirror image. If you see that the part of the graph on the right (positive) side of the y-axis matches the part of the graph on the left (negative) side of the y-axis, then the graph is symmetrical across the y-axis. If a function is symmetrical across the y-axis, then the function is even. You can test symmetry by selecting individual points. If the y-value for any selected x is the same as the y-value for -x, then the function is even. The points that were chosen above for plotting f ( x ) = 2 x 2 + 1 {\displaystyle f(x)=2x^{2}+1} f(x)=2x^{2}+1 gave the following results: (1,3) and (-1,3) (2,9) and (-2,9). The matching y-values for x=1 and x=-1 and for x=2 and x=-2 indicate that this is an even function. For a true test, selecting two points is not enough proof, but it is a good indication.

Test for origin symmetry. The origin is the central point (0,0). Origin symmetry means that a positive result for a chosen x-value will correspond to a negative result for -x, and vice versa. Odd functions display origin symmetry. If you select some sample values for x and their opposite corresponding -x values, you should get opposite results. Consider the function f ( x ) = x 3 + x {\displaystyle f(x)=x^{3}+x} f(x)=x^{3}+x. This function would provide the following points: f ( 1 ) = 1 3 + 1 = 1 + 1 = 2 {\displaystyle f(1)=1^{3}+1=1+1=2} f(1)=1^{3}+1=1+1=2. The point is (1,2). f ( − 1 ) = ( − 1 ) 3 + ( − 1 ) = − 1 − 1 = − 2 {\displaystyle f(-1)=(-1)^{3}+(-1)=-1-1=-2} f(-1)=(-1)^{3}+(-1)=-1-1=-2. The point is (-1,-2). f ( 2 ) = 2 3 + 2 = 8 + 2 = 10 {\displaystyle f(2)=2^{3}+2=8+2=10} f(2)=2^{3}+2=8+2=10. The point is (2,10). f ( − 2 ) = ( − 2 ) 3 + ( − 2 ) = − 8 − 2 = − 10 {\displaystyle f(-2)=(-2)^{3}+(-2)=-8-2=-10} f(-2)=(-2)^{3}+(-2)=-8-2=-10. The point is (-2,-10). Thus, f(x)=-f(-x), and you can conclude that the function is odd.

Look for no symmetry. The final example is a function that has no symmetry from side to side. If you look at the graph, it will not be a mirror image either across the y-axis or around the origin. Consider the function f ( x ) = x 2 + 2 x + 1 {\displaystyle f(x)=x^{2}+2x+1} f(x)=x^{2}+2x+1. Select some values for x and -x, as follows: f ( 1 ) = 1 2 + 2 ( 1 ) + 1 = 1 + 2 + 1 = 4 {\displaystyle f(1)=1^{2}+2(1)+1=1+2+1=4} f(1)=1^{2}+2(1)+1=1+2+1=4. The point to plot is (1,4). f ( − 1 ) = ( − 1 ) 2 + 2 ( − 1 ) + ( − 1 ) = 1 − 2 − 1 = − 2 {\displaystyle f(-1)=(-1)^{2}+2(-1)+(-1)=1-2-1=-2} f(-1)=(-1)^{2}+2(-1)+(-1)=1-2-1=-2. The point to plot is (-1,-2). f ( 2 ) = 2 2 + 2 ( 2 ) + 2 = 4 + 4 + 2 = 10 {\displaystyle f(2)=2^{2}+2(2)+2=4+4+2=10} f(2)=2^{2}+2(2)+2=4+4+2=10. The point to plot is (2,10). f ( − 2 ) = ( − 2 ) 2 + 2 ( − 2 ) + ( − 2 ) = 4 − 4 − 2 = − 2 {\displaystyle f(-2)=(-2)^{2}+2(-2)+(-2)=4-4-2=-2} f(-2)=(-2)^{2}+2(-2)+(-2)=4-4-2=-2. The point to plot is (2,-2). These should give you enough points already to note that there is no symmetry. The y-values for opposing pairs of x-values are neither the same nor are they opposites. This function is neither even nor odd. You may recognize that this function, f ( x ) = x 2 + 2 x + 1 {\displaystyle f(x)=x^{2}+2x+1} f(x)=x^{2}+2x+1, can be rewritten as f ( x ) = ( x + 1 ) 2 {\displaystyle f(x)=(x+1)^{2}} f(x)=(x+1)^{2}. Written in this form, it appears to be an even function because there is only one exponent, and that is an even number. However, this sample illustrates that you cannot determine whether a function is even or odd when it is written in a parenthetical form. You must expand the function into individual terms and then examine the exponents.