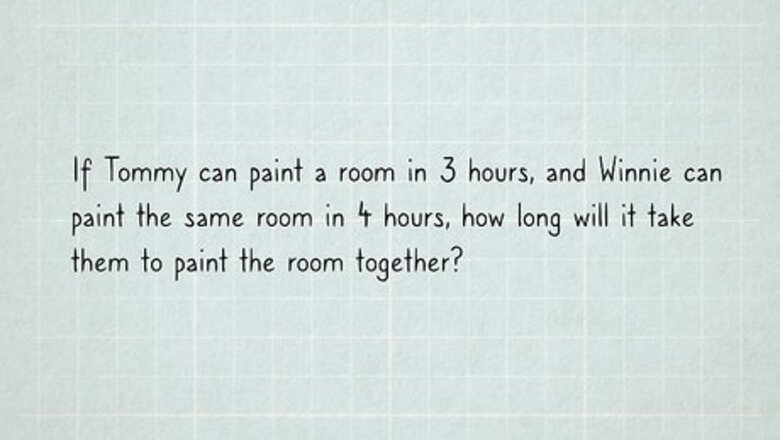
views
X
Research source
These are equations that involve at least one fraction. The problems basically require finding unit rates, combining them, and setting them equal to an unknown rate. These problems require a lot of interpretive logic, but as long as you know how to work with fractions, solving them is fairly easy.
Problems with Two People Working Together
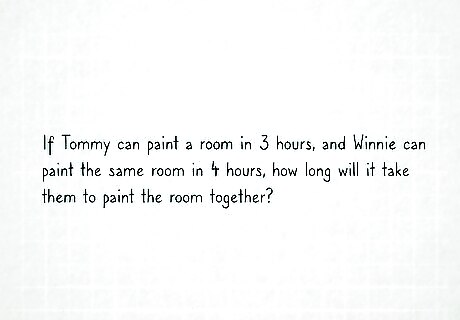
Read the problem carefully. Use this method if the problem represents two or more people working together to complete a job. The problem should also give you the amount of time it would take each person to complete the job alone. For example, the problem might ask, “If Tommy can paint a room in 3 hours, and Winnie can paint the same room in 4 hours, how long will it take them to paint the room together?

Determine the hourly rate of each individual. The hourly rate is represented by creating a fraction, where the total number of hours it takes to complete the job is the denominator (bottom number), and 1 is the numerator (top number). For example, if Tommy can paint a room in 3 hours, his hourly rate is 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}; that is, each hour he completes 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}} of a room. If Winnie takes 4 hours to paint a room, her hourly rate is 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}}.

Create a ratio for their combined hourly rate. This will be 1 t {\displaystyle {\frac {1}{t}}} {\frac {1}{t}}, where t {\displaystyle t} t equals the amount of time it takes them to complete the job together.

Set up the equation. Because they are working together, their combined hourly rate will equal the sum of their individual hourly rates. For example, if Tommy paints 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}} of a room in 1 hour, Winnie paints 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}} of a room in 1 hour, and together they complete 1 t {\displaystyle {\frac {1}{t}}} {\frac {1}{t}} of a room in 1 hour, the equation will be: 1 3 + 1 4 = 1 t {\displaystyle {\frac {1}{3}}+{\frac {1}{4}}={\frac {1}{t}}} {\frac {1}{3}}+{\frac {1}{4}}={\frac {1}{t}}.

Add the fractions together. You will need to find the least common denominator. For complete instructions on how to add fractions, you can read the article Add Fractions. For example, 12 is the least common denominator of 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}} and 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}}, thus: 1 3 + 1 4 = 1 t {\displaystyle {\frac {1}{3}}+{\frac {1}{4}}={\frac {1}{t}}} {\frac {1}{3}}+{\frac {1}{4}}={\frac {1}{t}} 4 12 + 3 12 = 1 t {\displaystyle {\frac {4}{12}}+{\frac {3}{12}}={\frac {1}{t}}} {\frac {4}{12}}+{\frac {3}{12}}={\frac {1}{t}} 7 12 = 1 t {\displaystyle {\frac {7}{12}}={\frac {1}{t}}} {\frac {7}{12}}={\frac {1}{t}}
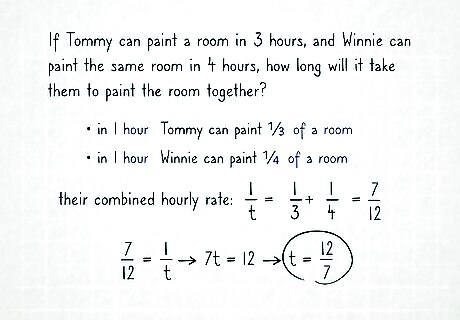
Solve for t {\displaystyle t} t. To do this, cross multiply. In this instance, you can also simply take the inverse of the fraction. For example: 7 12 = 1 t {\displaystyle {\frac {7}{12}}={\frac {1}{t}}} {\frac {7}{12}}={\frac {1}{t}} 7 t = 12 {\displaystyle 7t=12} 7t=12 t = 12 7 {\displaystyle t={\frac {12}{7}}} t={\frac {12}{7}}

Simplify the fraction, if necessary. This will give you the number of hours it takes for the workers to complete the job together. For example, if Tommy takes 3 hours to paint a room, and Winnie takes 4 hours to complete a room, together they can complete a room in 12 7 {\displaystyle {\frac {12}{7}}} {\frac {12}{7}}, or 1 5 7 {\displaystyle 1{\frac {5}{7}}} 1{\frac {5}{7}} of an hour. This equals almost two hours (about 1 hour, 43 minutes).
Problems with Two People Working Against Each Other

Read the problem carefully. Use this method if the problem represents one person (or thing) completing a job and another person (or thing) undoing the job the other person is doing. A typical problem involves pipes filling and draining a pool. For example, the problem might ask, “If a hose can fill a pool 6 hours, and an open drain can empty it in 2 hours, how long will it take the open drain to empty the pool with the hose on?”

Determine the hourly rate of the individual completing the job. Look at the problem carefully to determine which individual this is. If the goal is to empty something, the individual doing the draining is completing the job. The hourly rate is is represented by creating a fraction, where the total number hours it takes to complete the job is the denominator (bottom number), and 1 is the numerator (top number). For example, if a drain can empty a pool in 2 hours, and you need to calculate how long it takes to empty the pool, then the drain is completing the job. Its hourly rate is 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}; that is, each hour it empties 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} of the pool.

Determine the hourly rate of the individual undoing the job. Remember that the total number of hours it takes to undo the job will be in the denominator, and 1 will be in the numerator. For example, if the hose can fill a pool in 3 hours, but the goal is to empty the pool, then the hose is undoing the job. If the hose fills the pool in 6 hours, Its hourly rate is 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}}; that is, each hour it fills 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}} of the pool.

Create a ratio for their combined hourly rate. This will be 1 t {\displaystyle {\frac {1}{t}}} {\frac {1}{t}}, where t {\displaystyle t} t equals the amount of time it takes them to complete the job while working against each other.

Set up the equation. Because they are working against each other, their combined hourly rate will equal the difference between their individual hourly rates. This is the hourly rate of the individual completing the job minus the hourly rate of the individual undoing the job. For example, if a drain empties 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} of a pool in 1 hour, a hose fills 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}} of a pool in 1 hour, and together they empty 1 t {\displaystyle {\frac {1}{t}}} {\frac {1}{t}} of a pool in 1 hour, the equation will be: 1 2 − 1 6 = 1 t {\displaystyle {\frac {1}{2}}-{\frac {1}{6}}={\frac {1}{t}}} {\frac {1}{2}}-{\frac {1}{6}}={\frac {1}{t}}.

Subtract the fractions. You will need to find the least common denominator. For complete instructions on how to subtract fractions, you can read the article Subtract Fractions. For example, 6 is the least common denominator of 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} and 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}}, thus: 1 2 − 1 6 = 1 t {\displaystyle {\frac {1}{2}}-{\frac {1}{6}}={\frac {1}{t}}} {\frac {1}{2}}-{\frac {1}{6}}={\frac {1}{t}} 3 6 − 1 6 = 1 t {\displaystyle {\frac {3}{6}}-{\frac {1}{6}}={\frac {1}{t}}} {\frac {3}{6}}-{\frac {1}{6}}={\frac {1}{t}} 2 6 = 1 t {\displaystyle {\frac {2}{6}}={\frac {1}{t}}} {\frac {2}{6}}={\frac {1}{t}}

Solve for t {\displaystyle t} t by cross multiplying. Note that, In this instance, you can also simply take the inverse of the fraction. For example: 2 6 = 1 t {\displaystyle {\frac {2}{6}}={\frac {1}{t}}} {\frac {2}{6}}={\frac {1}{t}} 2 t = 6 {\displaystyle 2t=6} 2t=6 2 t = 6 {\displaystyle 2t=6} 2t=6 t = 6 2 {\displaystyle t={\frac {6}{2}}} t={\frac {6}{2}}

Simplify the fraction, if necessary. This will give you the number of hours it takes for the individuals to complete the job while working against each other. For example, if a hose fills a pool in 6 hours, and a drain empties the pool in 2 hours to, working against each other, the pool will drain in 6 2 {\displaystyle {\frac {6}{2}}} {\frac {6}{2}} hours, or 3 {\displaystyle 3} 3 hours.
Problems with Two People Working In Shifts

Read the problem carefully. Use this method if the problem represents two or more people (or things) working together to complete a job for a part of the time, and then just one individual (or thing) finishing (or starting) the job alone. The problem should also provide the hourly rate of each individual. For example, the problem might be: “Damarion can clean the cat shelter in 8 hours, and Cassandra can clean the shelter in 4 hours. They work together for 2 hours, but then Cassandra leaves to take some cats to the vet. How long will it take for Damarion to finish cleaning the shelter on his own?”

Determine the hourly rate of each individual. The hourly rate is is represented by creating a fraction, where the total number hours it takes to complete the job is the denominator (bottom number), and 1 is the numerator (top number). For example, if Damarion can clean the cat shelter in 8 hours, his hourly rate is 1 8 {\displaystyle {\frac {1}{8}}} {\frac {1}{8}}; that is, each hour he completes 1 8 {\displaystyle {\frac {1}{8}}} {\frac {1}{8}} of a room. If Cassandra takes 4 hours to clean the shelter, her hourly rate is 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}}.

Determine how much they can complete together in 1 hour. To do this, add their hourly rates together. For complete instructions on how to add fractions, read the article Add Fractions. For example, if Damarion cleans 1 8 {\displaystyle {\frac {1}{8}}} {\frac {1}{8}} of the room in an hour, and Cassandra completes 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}} of the room an hour, together they will complete 1 8 + 1 4 {\displaystyle {\frac {1}{8}}+{\frac {1}{4}}} {\frac {1}{8}}+{\frac {1}{4}} of the room in an hour: 1 8 + 1 4 {\displaystyle {\frac {1}{8}}+{\frac {1}{4}}} {\frac {1}{8}}+{\frac {1}{4}} = 2 16 + 4 16 {\displaystyle ={\frac {2}{16}}+{\frac {4}{16}}} ={\frac {2}{16}}+{\frac {4}{16}} = 6 16 {\displaystyle ={\frac {6}{16}}} ={\frac {6}{16}}

Calculate how much the workers completed together. To do this, multiply how much they complete in an hour by how many hours they worked together. For complete instructions on how to multiply fractions, read Multiply Fractions. For example, if Damarion and Cassandra together clean 6 16 {\displaystyle {\frac {6}{16}}} {\frac {6}{16}} of the shelter in 1 hour, in two hours they complete twice that much: 6 16 × 2 {\displaystyle {\frac {6}{16}}\times 2} {\frac {6}{16}}\times 2 = 12 16 {\displaystyle ={\frac {12}{16}}} ={\frac {12}{16}} = 3 4 {\displaystyle ={\frac {3}{4}}} ={\frac {3}{4}} of the shelter

Calculate how much of the job remains after one person leaves. To do this, subtract the fraction of what they did from 1 whole. For complete instructions on how to subtract fractions, read Subtract Fractions. For example, if Damarion and Cassandra cleaned 3 4 {\displaystyle {\frac {3}{4}}} {\frac {3}{4}} of the shelter in 2 hours, then after Cassandra leaves, Damarion has to clean 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}} of the shelter on his own.

Set up the equation. You are looking for how long it will take the work to be completed by the remaining individual. To do this, you need to multiply the individual’s hourly rate times the number of hours ( h {\displaystyle h} h) it will take to complete the job. This will be equal to the amount of the job that needs to be finished. For example, if Damarion cleans the shelter at a rate of 1 8 {\displaystyle {\frac {1}{8}}} {\frac {1}{8}} per hour, and he needs to complete 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}} of the job on his own, you equation will be 1 8 h = 1 4 {\displaystyle {\frac {1}{8}}h={\frac {1}{4}}} {\frac {1}{8}}h={\frac {1}{4}}, or, more simply, h 8 = 1 4 {\displaystyle {\frac {h}{8}}={\frac {1}{4}}} {\frac {h}{8}}={\frac {1}{4}}

Solve for h {\displaystyle h} h. To do this, cross multiply the two fractions. Make sure to simplify the fractions, if necessary. This will give you the number of hours it takes the remaining person to complete the job on his or her own. For example: h 8 = 1 4 {\displaystyle {\frac {h}{8}}={\frac {1}{4}}} {\frac {h}{8}}={\frac {1}{4}} 4 h = 8 {\displaystyle 4h=8} 4h=8 h = 2 {\displaystyle h=2} h=2So, it will take Damarion 2 hours to complete the job on his own.



















Comments
0 comment