
views
Solving a Problem with Exponents

Address the order of operations. Just like any problem in mathematics, an algebraic problem must be completed by the order of operations. You can use the phrase "Please Excuse My Dear Aunt Sally," or the acronym PEMDAS, to help you remember Parentheses, Exponents, Multiplication, Division, Addition, Subtraction. For example, if the problem is 4 ( x 10 ÷ x 4 ) ÷ 2 ( x 3 × x 2 ) − 3 x 0 {\displaystyle 4(x^{10}\div x^{4})\div 2(x^{3}\times x^{2})-3x^{0}} 4(x^{{10}}\div x^{{4}})\div 2(x^{{3}}\times x^{{2}})-3x^{{0}}, you would first complete the calculations inside the parentheses.

Simplify the expressions using the laws of exponents. Remember, you can only simplify if the exponents have the same base. For example, x 10 ÷ x 4 {\displaystyle x^{10}\div x^{4}} x^{{10}}\div x^{{4}} can simplify to x 10 − 4 {\displaystyle x^{10-4}} x^{{10-4}}, or x 6 {\displaystyle x^{6}} x^{6}. x 3 × x 2 {\displaystyle x^{3}\times x^{2}} x^{{3}}\times x^{{2}} can simplify to x 3 + 2 {\displaystyle x^{3+2}} x^{{3+2}}, or x 5 {\displaystyle x^{5}} x^{{5}}. x 0 {\displaystyle x^{0}} x^{{0}} is 1, since any number to the zero power is 1. So, the simplified problem becomes 4 ( x 6 ) ÷ 2 ( x 5 ) − 3 ( 1 ) {\displaystyle 4(x^{6})\div 2(x^{5})-3(1)} 4(x^{{6}})\div 2(x^{{5}})-3(1).

Simplify coefficients. Coefficients are the numbers in an algebraic problem. When simplifying coefficients with exponents, you complete the regular operations. For example, for 4 ( x 6 ) ÷ 2 ( x 5 ) {\displaystyle 4(x^{6})\div 2(x^{5})} 4(x^{{6}})\div 2(x^{{5}}), you would first divide the coefficients: 4 ÷ 2 = 2 {\displaystyle 4\div 2=2} 4\div 2=2. Then, divide the exponents: x 6 ÷ x 5 {\displaystyle x^{6}\div x^{5}} x^{{6}}\div x^{{5}}= x 6 − 5 {\displaystyle x^{6-5}} x^{{6-5}}= x 1 {\displaystyle x^{1}} x^{1}= x {\displaystyle x} x. Since 3 ( 1 ) {\displaystyle 3(1)} 3(1) simplifies to 3 {\displaystyle 3} 3, the final, simplified problem is 2 x − 3 {\displaystyle 2x-3} 2x-3.
Understanding the Laws of Exponents

Solve expressions with a positive exponent. An exponent simply tells you how many times you multiply the base (big number) by itself. For example, x 3 {\displaystyle x^{3}} x^{{3}} is the same as x × x × x {\displaystyle x\times x\times x} x\times x\times x. Plugging in a number, you would have 2 3 {\displaystyle 2^{3}} 2^{{3}}= 2 × 2 × 2 {\displaystyle 2\times 2\times 2} 2\times 2\times 2= 8 {\displaystyle 8} 8 Expressions to the first degree (expressions with an exponent of 1) always simplify to the base. It is like saying “x one time.” For example, x 1 = x {\displaystyle x^{1}=x} x^{1}=x. Expressions to the zero degree (expressions with an exponent of 0) always simplify to 1. For example, x 0 = 1 {\displaystyle x^{0}=1} x^{0}=1.

Simplify multiplication expressions with a positive exponent. When you multiply two exponents with the same base, you can simplify the expression by adding the exponents. Do NOT add or multiply the base. This rule does not apply to numbers that have a different base. For example, you cannot simplify 2 3 × 3 2 {\displaystyle 2^{3}\times 3^{2}} 2^{{3}}\times 3^{{2}}, you simply have to solve the exponents separately and then multiply the two numbers. For example, x 2 × x 4 {\displaystyle x^{2}\times x^{4}} x^{{2}}\times x^{{4}} is the same as x 2 + 4 {\displaystyle x^{2+4}} x^{{2+4}}, which is the same as x 6 {\displaystyle x^{6}} x^{{6}}. Plugging in a number, you would have 2 2 × 2 4 {\displaystyle 2^{2}\times 2^{4}} 2^{{2}}\times 2^{{4}}= 2 2 + 4 {\displaystyle 2^{2+4}} 2^{{2+4}}= 2 6 {\displaystyle 2^{6}} 2^{{6}}= 2 × 2 × 2 × 2 × 2 × 2 {\displaystyle 2\times 2\times 2\times 2\times 2\times 2} 2\times 2\times 2\times 2\times 2\times 2= 64 {\displaystyle 64} 64

Simplify division expressions with a positive exponent. When you divide to exponents with the same base, you can simplify the expression by subtracting the exponents. Do NOT divide or subtract the base. For example, x 10 x 5 {\displaystyle {\frac {x^{10}}{x^{5}}}} {\frac {x^{{10}}}{x^{{5}}}} is the same as x 10 − 5 {\displaystyle x^{10-5}} x^{{10-5}}, which is the same as x 5 {\displaystyle x^{5}} x^{5}. Plugging in a number, you would have 2 10 2 5 {\displaystyle {\frac {2^{10}}{2^{5}}}} {\frac {2^{{10}}}{2^{{5}}}}= 2 10 − 5 {\displaystyle 2^{10-5}} 2^{{10-5}}= 2 5 {\displaystyle 2^{5}} 2^{5}= 2 × 2 × 2 × 2 × 2 {\displaystyle 2\times 2\times 2\times 2\times 2} 2\times 2\times 2\times 2\times 2= 32 {\displaystyle 32} 32

Simplify exponents with a positive exponent. Sometimes an exponent will have an exponent. In this situation, you would multiply the two exponents. For example, ( x 2 ) 3 {\displaystyle (x^{2})^{3}} (x^{{2}})^{{3}} is the same as x 2 × 3 {\displaystyle x^{2\times 3}} x^{{2\times 3}}, which is the same as x 6 {\displaystyle x^{6}} x^{{6}}. Plugging in a number, you would have ( 2 2 ) 3 {\displaystyle (2^{2})^{3}} (2^{{2}})^{{3}}= 2 2 × 3 {\displaystyle 2^{2\times 3}} 2^{{2\times 3}}= 2 6 {\displaystyle 2^{6}} 2^{{6}}= 2 × 2 × 2 × 2 × 2 × 2 {\displaystyle 2\times 2\times 2\times 2\times 2\times 2} 2\times 2\times 2\times 2\times 2\times 2= 64 {\displaystyle 64} 64
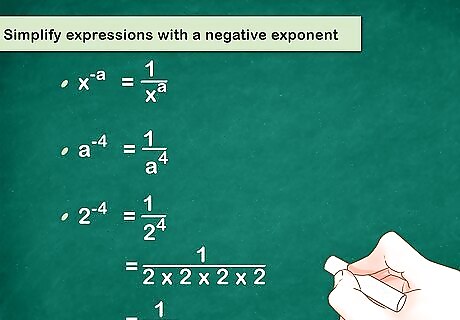
Simplify expressions with a negative exponent. You can think of a negative exponent as being the opposite of a positive exponent. Since a positive exponent tells you how many times to multiply, a negative exponent tells you how many times to divide. To simplify an expression with a negative exponent, use the formula x − a = 1 x a {\displaystyle x^{-a}={\frac {1}{x^{a}}}} x^{{-a}}={\frac {1}{x^{{a}}}}. For example, x − 4 {\displaystyle x^{-4}} x^{{-4}} is the same as 1 x 4 {\displaystyle {\frac {1}{x^{4}}}} {\frac {1}{x^{{4}}}}. Plugging in a number, 2 − 4 {\displaystyle 2^{-4}} 2^{{-4}}= 1 2 4 {\displaystyle {\frac {1}{2^{4}}}} {\frac {1}{2^{{4}}}}= 1 2 × 2 × 2 × 2 {\displaystyle {\frac {1}{2\times 2\times 2\times 2}}} {\frac {1}{2\times 2\times 2\times 2}}= 1 16 {\displaystyle {\frac {1}{16}}} {\frac {1}{16}}



















Comments
0 comment