How to Calculate Speed in Metres per Second

Calculating Speed Given Distance and Time

Set up the formula for speed. The formula is speed = distance time {\displaystyle {\text{speed}}={\frac {\text{distance}}{\text{time}}}} {\text{speed}}={\frac {{\text{distance}}}{{\text{time}}}}. The distance refers to how far something or someone traveled, and the time refers to how long it took to travel that distance.

Plug the total distance into the formula. This information should be given in meters. Sometimes, however, you might need to calculate the distance traveled using information provided in the problem, or you might need to convert another unit, such as miles, feet, or kilometers, into meters. For example, you might know that Henry drove his car for 48,000 meters. So, your formula will look like this: speed = 48 , 000 time {\displaystyle {\text{speed}}={\frac {48,000}{\text{time}}}} {\text{speed}}={\frac {48,000}{{\text{time}}}}.

Plug the total time into the formula. Sometimes this information will be given; sometimes you need to calculate the time given a beginning and ending time. Find the difference between the beginning and ending time to find the total time it took to travel. In these instances, you will likely need to convert minutes traveled into seconds traveled by multiplying the number of minutes traveled by 60. For example, you might know that Henry began driving at 6:00p.m. He drove 48,000 meters, and arrived at his destination at 6:30 p.m. The difference between 6:00p.m. and 6:30p.m. is 30 minutes. To find the number of seconds, calculate 30 × 60 = 1 , 800 {\displaystyle 30\times 60=1,800} 30\times 60=1,800. So, Henry traveled for 1,800 seconds. You formula should look like this: speed = 48 , 000 1 , 800 {\displaystyle {\text{speed}}={\frac {48,000}{1,800}}} {\text{speed}}={\frac {48,000}{1,800}}.

Divide the distance by the time. This will give you the speed in meters per second. For example, speed = 48 , 000 1 , 800 = 26.67 m / s {\displaystyle {\text{speed}}={\frac {48,000}{1,800}}=26.67m/s} {\text{speed}}={\frac {48,000}{1,800}}=26.67m/s.

Calculating Speed Using a Distance-Time Graph

Set up the formula for speed. The formula is speed = distance time {\displaystyle {\text{speed}}={\frac {\text{distance}}{\text{time}}}} {\text{speed}}={\frac {{\text{distance}}}{{\text{time}}}}.

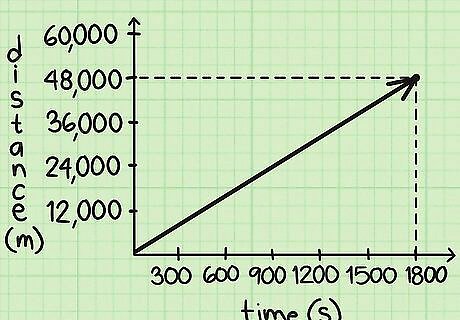
Acquire your distance-time graph. This should be presented to you in the form of a coordinate plane, and the graph should have at least one line plotted. The line represents the distance and time traveled by a single person or object. If the graph has multiple lines, each line represents a different person or object. The first endpoint of the line signifies when the person or object started moving. The second endpoint of the line signifies when the person or object stopped moving.

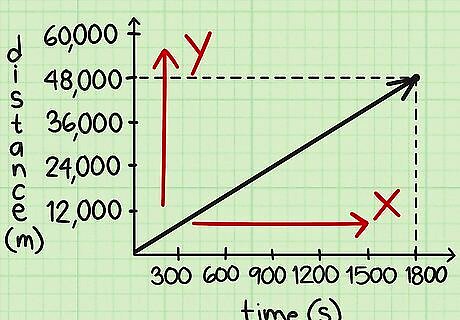
Interpret the x-axis and the y-axis of the graph. The x-axis is the horizontal axis, and it indicates the time spent travelling. The y-axis is the vertical axis, and it indicates the distance traveled. If the units of the graph are not listed in terms of meters per second, you will need to convert the units after you find the speed. The steeper the line on a distance-time graph, the faster the speed. A horizontal line indicates that there was no change in distance. This would indicate a speed of 0 meters per second.

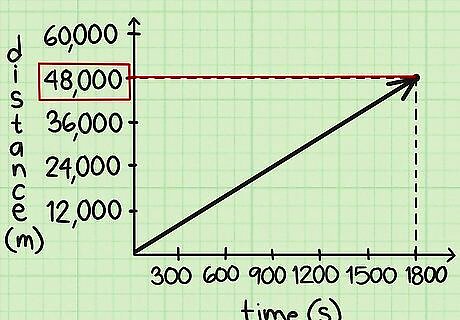
Calculate the distance traveled by the person or object. To calculate the distance, find the appropriate line on the graph and note the point where the line ends. Find the y-coordinate of this point by moving your finger horizontally to the y-axis. This will show you the distance travelled. If the line does not start at the (0, 0) point, you need to find the distance by subtracting the y-values of the two endpoints of the line. For example, if the line showing the distance and time traveled by Henry begins at (0, 0) and ends at the point (1,800, 48,000), the number of meters traveled is 48,000.

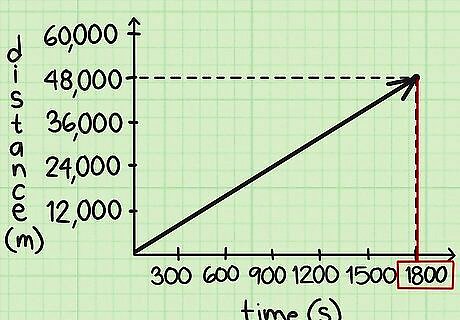
Calculate the time spent travelling by the person or object. To calculate the time, go back to the point where the line ends. Find the x-coordinate of this point by moving your finger vertically to the x-axis. This will show you the time spent traveling. For example, if the line showing the distance and time traveled by Henry ends at the point (1,800, 48,000), the number of seconds traveled is 1,800.

Divide the distance by the time. Plug the two values into the formula and divide. This will give you the speed. If the units on the graph were listed in units other than meters per second, you will need to convert the units to find the speed in meters per second. For example, speed = 48 , 000 1 , 800 = 26.67 m / s {\displaystyle {\text{speed}}={\frac {48,000}{1,800}}=26.67m/s} {\text{speed}}={\frac {48,000}{1,800}}=26.67m/s.

Converting Miles Per Hour to Meters Per Second

Calculate the speed in miles per hour. Do this using the formula speed = distance time {\displaystyle {\text{speed}}={\frac {\text{distance}}{\text{time}}}} {\text{speed}}={\frac {{\text{distance}}}{{\text{time}}}}. Restate the speed as a ratio of miles over 1 hour. For example, if Becky drove 50 miles in 1.25 hours at a constant speed, you would find the speed by calculating speed = 50 miles 1.25 hours = 40 m p h {\displaystyle {\text{speed}}={\frac {50\;{\text{miles}}}{1.25\;{\text{hours}}}}=40mph} {\text{speed}}={\frac {50\;{\text{miles}}}{1.25\;{\text{hours}}}}=40mph. As a ratio, you would state the speed as 40 miles 1 hour {\displaystyle {\frac {40\;{\text{miles}}}{1\;{\text{hour}}}}} {\frac {40\;{\text{miles}}}{1\;{\text{hour}}}}.

Convert miles per hour to miles per minute. To do this set up fractions to cancel the units. To cancel units, you need to multiply two fractions that share one unit, but not the other. In order for the unit to cancel, it needs to be in the numerator of one fraction, and the denominator of the other fraction. Since there are 60 minutes in 1 hour, you would multiply the speed in miles per hour by the fraction 1 hour 60 minutes {\displaystyle {\frac {1\;{\text{hour}}}{60\;{\text{minutes}}}}} {\frac {1\;{\text{hour}}}{60\;{\text{minutes}}}}. For example: 40 miles 1 hour × 1 hour 60 minutes {\displaystyle {\frac {40\;{\text{miles}}}{1\;{\text{hour}}}}\times {\frac {1\;{\text{hour}}}{60\;{\text{minutes}}}}} {\frac {40\;{\text{miles}}}{1\;{\text{hour}}}}\times {\frac {1\;{\text{hour}}}{60\;{\text{minutes}}}} 40 miles 1 hour × 1 hour 60 minutes {\displaystyle {\frac {40\;{\text{miles}}}{1\;{\cancel {\text{hour}}}}}\times {\frac {1\;{\cancel {\text{hour}}}}{60\;{\text{minutes}}}}} {\frac {40\;{\text{miles}}}{1\;{\cancel {{\text{hour}}}}}}\times {\frac {1\;{\cancel {{\text{hour}}}}}{60\;{\text{minutes}}}} 40 × 1 miles 1 × 60 minutes {\displaystyle {\frac {40\times 1\;{\text{miles}}}{1\times 60\;{\text{minutes}}}}} {\frac {40\times 1\;{\text{miles}}}{1\times 60\;{\text{minutes}}}} 40 miles 60 minutes {\displaystyle {\frac {40\;{\text{miles}}}{60\;{\text{minutes}}}}} {\frac {40\;{\text{miles}}}{60\;{\text{minutes}}}}

Convert miles per minute to miles per second. Do this just as you did for the previous conversion. Multiply the two ratios to cancel units. There are 60 seconds in 1 minute, so your second fraction will be 1 minute 60 seconds {\displaystyle {\frac {1\;{\text{minute}}}{60\;{\text{seconds}}}}} {\frac {1\;{\text{minute}}}{60\;{\text{seconds}}}}. For example: 40 miles 60 minutes × 1 minute 60 seconds {\displaystyle {\frac {40\;{\text{miles}}}{60\;{\text{minutes}}}}\times {\frac {1\;{\text{minute}}}{60\;{\text{seconds}}}}} {\frac {40\;{\text{miles}}}{60\;{\text{minutes}}}}\times {\frac {1\;{\text{minute}}}{60\;{\text{seconds}}}} 40 miles 60 minutes × 1 minute 60 seconds {\displaystyle {\frac {40\;{\text{miles}}}{60\;{\cancel {\text{minutes}}}}}\times {\frac {1\;{\cancel {\text{minute}}}}{60\;{\text{seconds}}}}} {\frac {40\;{\text{miles}}}{60\;{\cancel {{\text{minutes}}}}}}\times {\frac {1\;{\cancel {{\text{minute}}}}}{60\;{\text{seconds}}}} 40 × 1 miles 60 × 60 seconds {\displaystyle {\frac {40\times 1\;{\text{miles}}}{60\times 60\;{\text{seconds}}}}} {\frac {40\times 1\;{\text{miles}}}{60\times 60\;{\text{seconds}}}} 40 miles 3600 seconds {\displaystyle {\frac {40\;{\text{miles}}}{3600\;{\text{seconds}}}}} {\frac {40\;{\text{miles}}}{3600\;{\text{seconds}}}}

Convert miles per second to feet per second. There are 5,280 feet in a mile. Thus, you will multiply the ratio of miles per second by 5280 feet 1 mile {\displaystyle {\frac {5280\;{\text{feet}}}{1\;{\text{mile}}}}} {\frac {5280\;{\text{feet}}}{1\;{\text{mile}}}}. For example: 40 miles 3600 seconds × 5280 feet 1 mile {\displaystyle {\frac {40\;{\text{miles}}}{3600\;{\text{seconds}}}}\times {\frac {5280\;{\text{feet}}}{1\;{\text{mile}}}}} {\frac {40\;{\text{miles}}}{3600\;{\text{seconds}}}}\times {\frac {5280\;{\text{feet}}}{1\;{\text{mile}}}} 40 miles 3600 seconds × 5280 feet 1 mile {\displaystyle {\frac {40\;{\cancel {\text{miles}}}}{3600\;{\text{seconds}}}}\times {\frac {5280\;{\text{feet}}}{1\;{\cancel {\text{mile}}}}}} {\frac {40\;{\cancel {{\text{miles}}}}}{3600\;{\text{seconds}}}}\times {\frac {5280\;{\text{feet}}}{1\;{\cancel {{\text{mile}}}}}} 40 × 5280 feet 3600 × 1 seconds {\displaystyle {\frac {40\times 5280\;{\text{feet}}}{3600\times 1\;{\text{seconds}}}}} {\frac {40\times 5280\;{\text{feet}}}{3600\times 1\;{\text{seconds}}}} 211 , 200 feet 3600 seconds {\displaystyle {\frac {211,200\;{\text{feet}}}{3600\;{\text{seconds}}}}} {\frac {211,200\;{\text{feet}}}{3600\;{\text{seconds}}}}

Convert feet per second to meters per seconds. There are 3.28084 feet in 1 meter. So, you will multiply the ratio of feet per second by 1 meter 3.28084 feet {\displaystyle {\frac {1\;{\text{meter}}}{3.28084\;{\text{feet}}}}} {\frac {1\;{\text{meter}}}{3.28084\;{\text{feet}}}}. For example: 211 , 200 feet 3600 seconds × 1 meter 3.28084 feet {\displaystyle {\frac {211,200\;{\text{feet}}}{3600\;{\text{seconds}}}}\times {\frac {1\;{\text{meter}}}{3.28084\;{\text{feet}}}}} {\frac {211,200\;{\text{feet}}}{3600\;{\text{seconds}}}}\times {\frac {1\;{\text{meter}}}{3.28084\;{\text{feet}}}} 211 , 200 feet 3600 seconds × 1 meter 3.28084 feet {\displaystyle {\frac {211,200\;{\cancel {\text{feet}}}}{3600\;{\text{seconds}}}}\times {\frac {1\;{\text{meter}}}{3.28084\;{\cancel {\text{feet}}}}}} {\frac {211,200\;{\cancel {{\text{feet}}}}}{3600\;{\text{seconds}}}}\times {\frac {1\;{\text{meter}}}{3.28084\;{\cancel {{\text{feet}}}}}} 211 , 200 × 1 meters 3600 × 3.28084 seconds {\displaystyle {\frac {211,200\times 1\;{\text{meters}}}{3600\times 3.28084\;{\text{seconds}}}}} {\frac {211,200\times 1\;{\text{meters}}}{3600\times 3.28084\;{\text{seconds}}}} 211 , 200 meters 11 , 811 seconds {\displaystyle {\frac {211,200\;{\text{meters}}}{11,811\;{\text{seconds}}}}} {\frac {211,200\;{\text{meters}}}{11,811\;{\text{seconds}}}}.

Divide the numerator by the denominator. This will give you the speed in meters per second. For example, 211 , 200 11 , 811 = 17.88 {\displaystyle {\frac {211,200}{11,811}}=17.88} {\frac {211,200}{11,811}}=17.88. So, Becky drove at a rate of 17.88 meters per second.

Original news source