
views
- To find doubling time, you can use the Rule of 70.
- Check that the growth rate is under 0.15 so that it's small enough to use the rule.
- The Rule of 70 is derived from the basic continuous growth rate formula.
Estimating Doubling Time with the Rule of 70

Check that the growth rate is small enough for this method. Doubling time is a concept used for quantities that grow exponentially. Interest rates and the growth of a population are the most common examples used. If the growth rate is less than about 0.15 per time interval, we can use this fast method for a good estimate. If the problem doesn't give you the growth rate, you can find it in decimal form using C u r r e n t Q u a n t i t y − P a s t Q u a n t i t y P a s t Q u a n t i t y {\displaystyle {\frac {CurrentQuantity-PastQuantity}{PastQuantity}}} {\frac {CurrentQuantity-PastQuantity}{PastQuantity}}. Example 1: The population of an island grows at an exponential rate. From 2015 to 2016, the population increases from 20,000 to 22,800. What is the population's growth rate? 22,800 - 20,000 = 2,800 new people. 2,800 ÷ 20,000 = 0.14, so the population is growing by 0.14 per year. This is small enough that the estimate will be fairly accurate.
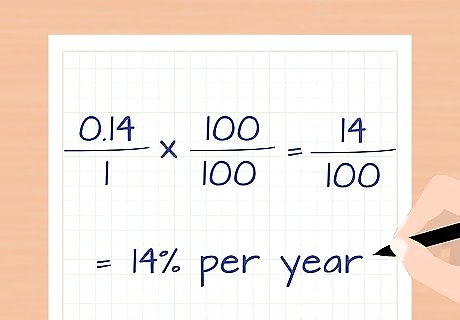
Multiply the growth rate by 100 to express it as a percentage. Most people find this more intuitive than the decimal fraction. Example 1 (cont): The island had a growth rate of 0.14, written as a decimal fraction. This represents 0.14 1 {\displaystyle {\frac {0.14}{1}}} {\frac {0.14}{1}}. Multiply the numerator and denominator by 100 to get 0.14 1 x 100 100 = 14 100 = {\displaystyle {\frac {0.14}{1}}x{\frac {100}{100}}={\frac {14}{100}}=} {\frac {0.14}{1}}x{\frac {100}{100}}={\frac {14}{100}}= 14% per year.

Divide 70 by the percentage growth rate. The answer will be the number of time intervals it takes the quantity to double. Make sure you express the growth rate as a percentage, not a decimal, or your answer will be off. (If you're curious why this "rule of 70" works, read the more detailed method below.) Example 1 (cont): The growth rate was 14%, so the number of time intervals required is 70 14 = 5 {\displaystyle {\frac {70}{14}}=5} {\frac {70}{14}}=5.
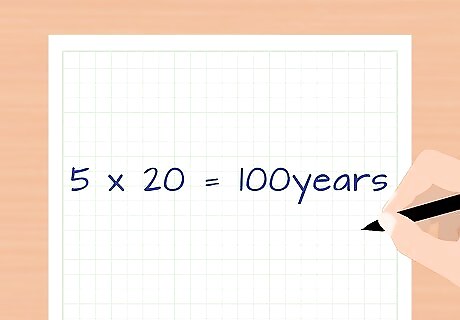
Convert your answer to the desired unit of time. In most cases, you'll already have the answer in terms of years, seconds, or another convenient measurement. If you measured the growth rate across a larger span of time, however, you may want to multiply to get your answer in terms of single units of time. Example 1 (cont): In this case, since we measured the growth across one year, each time interval is one year. The island population doubles every 5 years. Example 2: The second, spider-infested island nearby is much less popular. It also grew from a population of 20,000 to 22,800, but took 20 years to do it. Assuming its growth is exponential, what is this population's doubling time? This island has a 14% growth rate over 20 years. The "rule of 70" tells us it will also take 5 time intervals to double, but in this case each time interval is 20 years. (5 time intervals) x (20 /time interval) = 100 years for the spider-infested island's population to double.
Deriving the "Rule of 70" Formula
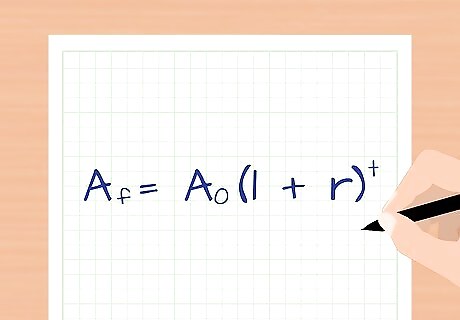
Understand the exponential growth rate formula. If you start with an initial amount A 0 {\displaystyle A_{0}} A_{0} that grows exponentially, the final amount A f {\displaystyle A_{f}} A_{f} is described by the formula A f = A 0 ( 1 + r ) t {\displaystyle A_{f}=A_{0}(1+r)^{t}} A_{f}=A_{0}(1+r)^{{t}}. The variable r represents the growth rate per time period (as a decimal), and t is the number of time periods. To make sense of this formula, picture a $100 investment with a 0.02 annual interest rate. Every time you calculate growth, you multiply the amount you have by 1.02. After one year, that's ($100)(1.02), after two years that's ($100)(1.02)(1.02), and so on. This simplifies to ( 1.02 ) t {\displaystyle (1.02)^{t}} (1.02)^{t}, where t is the number of time periods. Note: If r and t do not use the same time unit, use the formula A f = A 0 ( 1 + r n ) n t {\displaystyle A_{f}=A_{0}(1+{\frac {r}{n}})^{nt}} A_{f}=A_{0}(1+{\frac {r}{n}})^{{nt}}, where n is the number of times growth is calculated per time period. For example, if r = 0.05 per month and t = 4 years, use n = 12, since there are twelve months in a year.
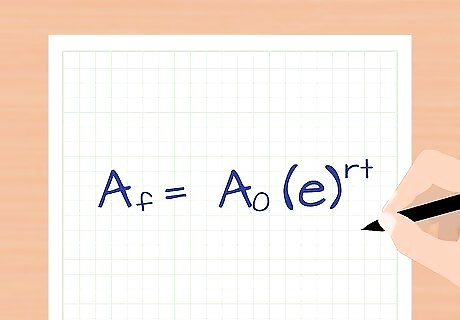
Rewrite this formula for continuous growth. In most real-world situations, a quantity grows "continuously" instead of increasing only at regular intervals. In this case, the formula for growth is A f = A 0 ( e ) r t {\displaystyle A_{f}=A_{0}(e)^{rt}} A_{f}=A_{0}(e)^{{rt}}, using the mathematical constant e. This formula is often used to approximate population growth, and always when calculating continuously compounded interest. In situations where growth is calculated at regular intervals, such as annually compounded interest, the formula above is more accurate. You can derive this from the formula from the one above using calculus concepts.

Plug in values for a doubled population. When the population doubles, the final amount A f {\displaystyle A_{f}} A_{f} will equal twice the initial amount, or 2 A 0 {\displaystyle 2A_{0}} 2A_{0}. Plug this into the formula and remove all A terms using algebra: 2 A 0 = A 0 ( e ) r t {\displaystyle 2A_{0}=A_{0}(e)^{rt}} 2A_{0}=A_{0}(e)^{{rt}} Divide both sides by A 0 {\displaystyle A_{0}} A_{0} 2 = e r t {\displaystyle 2=e^{rt}} 2=e^{{rt}}
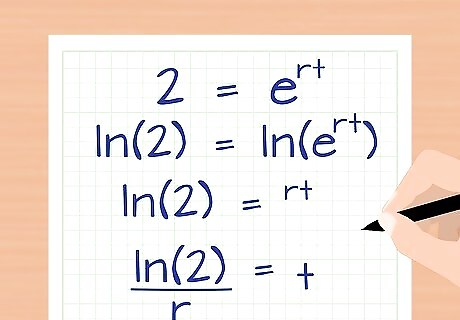
Rearrange to solve for t. If you haven't learned about logarithms yet, you may not know how to get the t out of the exponent. The term l o g m ( n ) {\displaystyle log_{m}(n)} log_{m}(n) means "the exponent m is raised by to get n." Because the constant e comes up so often in real world situations, there's a special term "natural log," abbreviated "ln," that means l o g e {\displaystyle log_{e}} log_{e}. Use this to isolate t on one side of the equation: 2 = e r t {\displaystyle 2=e^{rt}} 2=e^{{rt}} l n ( 2 ) = l n ( e r t ) {\displaystyle ln(2)=ln(e^{rt})} ln(2)=ln(e^{{rt}}) l n ( 2 ) = r t {\displaystyle ln(2)=rt} ln(2)=rt l n ( 2 ) r = t {\displaystyle {\frac {ln(2)}{r}}=t} {\frac {ln(2)}{r}}=t

Plug in growth rate and solve. Now you can solve for t by entering the decimal growth rate r into this formula. Notice that ln(2) is approximately equal to 0.69. Once you convert the growth rate from decimal to percentage form, you can round this value to get the "rule of 70" formula. Now that you know this formula, you can adjust it to solve similar problems. For example, find "tripling time" with the formula t t r i p l e = l n ( 3 ) r {\displaystyle t_{triple}={\frac {ln(3)}{r}}} t_{{triple}}={\frac {ln(3)}{r}}.



















Comments
0 comment