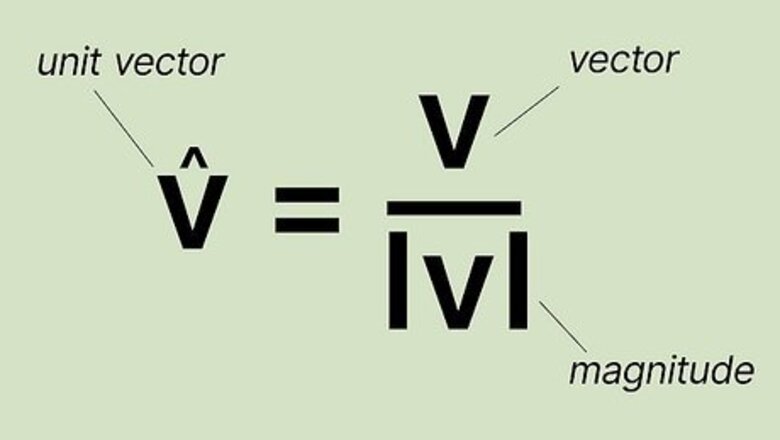
views
- A unit vector is a vector with a magnitude of 1. Unit vectors are marked with a cap symbol, which looks like a little arrow pointing upward: ^.
- To calculate a unit vector, divide the vector by its magnitude . In other words, follow this formula: .
- A vector is an object containing both magnitude and direction. The magnitude of a vector refers to the vector’s length.
Unit Vector Formula
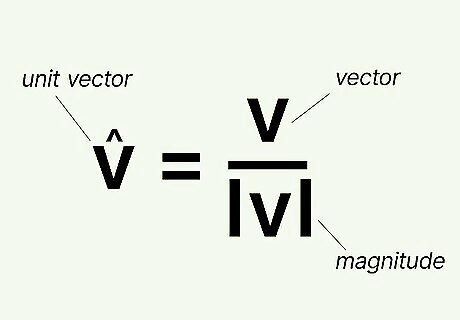
The formula to find unit vector is v ^ = v | v | {\displaystyle {\widehat {v}}={\tfrac {v}{|v|}}} {\displaystyle {\widehat {v}}={\tfrac {v}{|v|}}}. You can calculate the unit vector v ^ {\displaystyle {\widehat {v}}} {\displaystyle {\widehat {v}}} of any vector by dividing the vector by its magnitude | v | {\displaystyle |v|} {\displaystyle |v|}. For instance, to calculate the unit vector of vector a {\displaystyle a} a, you would follow this equation: a ^ = a | a | {\displaystyle {\widehat {a}}={\tfrac {a}{|a|}}} {\displaystyle {\widehat {a}}={\tfrac {a}{|a|}}}.
How to Calculate a Unit Vector
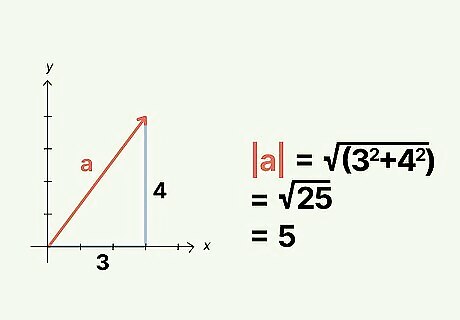
Identify the magnitude of the vector. The magnitude of a vector a {\displaystyle a} a is notated as | a | {\displaystyle |a|} {\displaystyle |a|}. To identify the magnitude of a 2-dimensional vector, you must first identify the horizontal and vertical components of the vector—that is, identify the coordinates of the vector along the x-axis and y-axis (for instance, 3 on the x-axis and 4 on the y-axis, usually notated as i ^ {\displaystyle {\widehat {i}}} {\displaystyle {\widehat {i}}} and j ^ {\displaystyle {\widehat {j}}} {\displaystyle {\widehat {j}}}, respectively) and find the sum of the squares of each of the components (which would be expressed as 3 2 + 4 2 {\displaystyle 3^{2}+4^{2}} {\displaystyle 3^{2}+4^{2}}). Take that sum, and find its square root in order to determine the magnitude. In other words, | a | {\displaystyle |a|} {\displaystyle |a|} = √ ( 3 2 + 4 2 ) {\displaystyle (3^{2}+4^{2})} {\displaystyle (3^{2}+4^{2})} = √ 25 {\displaystyle 25} 25 = 5 {\displaystyle 5} 5. To determine the magnitude of a 3-dimensional vector, follow the exact same formula, except add the z-axis—that is, the axis that usually intersects with the x- and y-axes diagonally (notated as k ^ {\displaystyle {\widehat {k}}} {\displaystyle {\widehat {k}}}). For instance, if 3-dimensional vector a {\displaystyle a} a = 3 i ^ + 4 j ^ + 5 k ^ {\displaystyle 3{\widehat {i}}+4{\widehat {j}}+5{\widehat {k}}} {\displaystyle 3{\widehat {i}}+4{\widehat {j}}+5{\widehat {k}}}, you would determine | a | {\displaystyle |a|} {\displaystyle |a|} using the following equation: | a | {\displaystyle |a|} {\displaystyle |a|} = √ ( 3 2 + 4 2 + 5 2 ) {\displaystyle (3^{2}+4^{2}+5^{2})} {\displaystyle (3^{2}+4^{2}+5^{2})}.
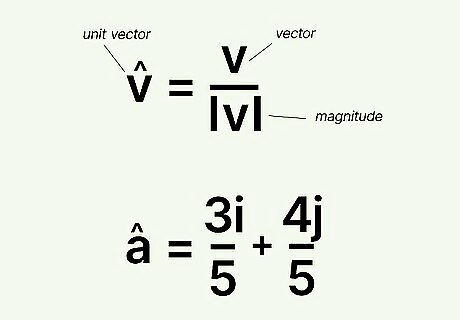
Divide the vector by its magnitude. Once you’ve determined the magnitude of the vector, take the vector and divide it by its magnitude. So if vector a {\displaystyle a} a is ( 3 , 4 ) {\displaystyle (3,4)} {\displaystyle (3,4)}, then a {\displaystyle a} a = ( 3 , 4 ) 5 {\displaystyle {\tfrac {(3,4)}{5}}} {\displaystyle {\tfrac {(3,4)}{5}}} = ( 3 5 {\displaystyle {\tfrac {3}{5}}} {\displaystyle {\tfrac {3}{5}}}, 4 5 {\displaystyle {\tfrac {4}{5}}} {\displaystyle {\tfrac {4}{5}}}). The unit vector, then, is ( 3 i ^ 5 + 4 j ^ 5 {\displaystyle {\tfrac {3{\widehat {i}}}{5}}+{\tfrac {4{\widehat {j}}}{5}}} {\displaystyle {\tfrac {3{\widehat {i}}}{5}}+{\tfrac {4{\widehat {j}}}{5}}}).
What is a vector?
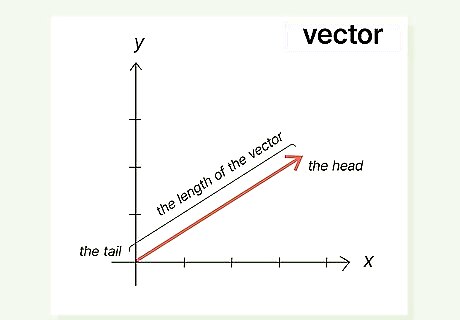
A vector is an object that contains both direction and magnitude. A vector is represented as a line on the Cartesian coordinate system, and it is denoted as a set of numbers representing its relationship to the x-axis (the vertical line on the graph) and the y-axis (the horizontal line). A vector’s magnitude refers to the size of the vector and is represented by a line with an arrow on the end. The length of the line denotes the length of the vector, while the direction of the arrow denotes the direction of the vector. Vectors possess both a starting point (the tail) and an ending point (the head, where the arrow is). The vector is identified by its intersecting axes, the x-axis (usually represented by the mathematical notation i {\displaystyle i} i) and the y-axis (notated as j {\displaystyle j} j). Thus, the vector v {\displaystyle v} v may be formulated as v {\displaystyle v} v = ( i , j ) {\displaystyle (i,j)} {\displaystyle (i,j)}. Vectors are used in various arithmetic operations including addition, subtraction, and multiplication. Vectors are also sometimes called Euclidean vectors, geometric vectors, or spatial vectors.
What is a unit vector?
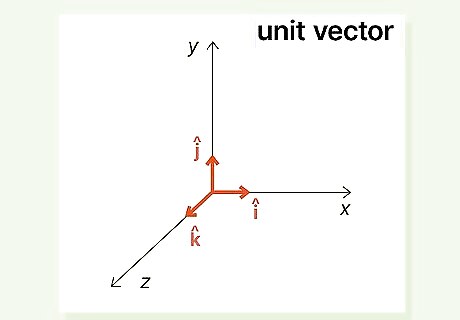
A unit vector is a vector with a magnitude of 1. Unit vectors, also called direction vectors, are used to describe the direction of a given vector—or, the angle the vector makes on an x-axis. Unit vectors are marked with a cap symbol, which looks like a little arrow pointing upward: ^. For example, if i {\displaystyle i} i, j {\displaystyle j} j, and k {\displaystyle k} k are the unit vectors in the directions of the x-axis, the y-axis, and the z-axis, they would be denoted as i ^ {\displaystyle {\widehat {i}}} {\displaystyle {\widehat {i}}}, j ^ {\displaystyle {\widehat {j}}} {\displaystyle {\widehat {j}}}, and k ^ {\displaystyle {\widehat {k}}} {\displaystyle {\widehat {k}}}, respectively.
What is the magnitude of a vector?
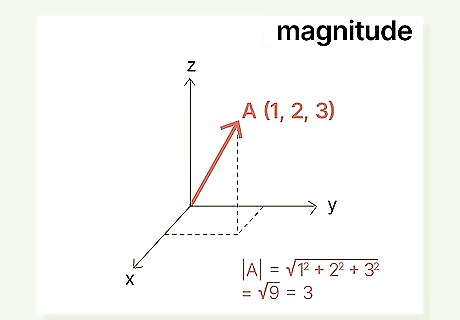
The magnitude is the length or size of the vector. A vector’s magnitude, also called its norm, denotes its length on an x-axis (or the vertical line on the graph on which the vector appears), giving it numeric value. The magnitude on summarizes the length of the vector on the x-axis, y-axis (the horizontal line), and z-axis. Magnitude is denoted as 2 vertical lines, one on each side of the vector: | v | {\displaystyle |v|} {\displaystyle |v|}. To calculate the magnitude of a given vector with the direction of the x-axis, y-axis, or z-axis, follow the Pythagorean Theorem: add the squares of the vector’s direction ratios. Then, calculate the square root of that sum. The magnitude of i ^ {\displaystyle {\widehat {i}}} {\displaystyle {\widehat {i}}} would be | i | {\displaystyle |i|} {\displaystyle |i|}, the magnitude of j ^ {\displaystyle {\widehat {j}}} {\displaystyle {\widehat {j}}} would be | j | {\displaystyle |j|} {\displaystyle |j|}, and the magnitude of k ^ {\displaystyle {\widehat {k}}} {\displaystyle {\widehat {k}}} would be | k | {\displaystyle |k|} {\displaystyle |k|}. To find the magnitude of vector A {\displaystyle A} A, where A {\displaystyle A} A = a i + b j + c k {\displaystyle ai+bj+ck} {\displaystyle ai+bj+ck} (and where i {\displaystyle i} i, j {\displaystyle j} j, and k {\displaystyle k} k represent the x-axis, y-axis, and z-axis, respectively), use the following equation: | A | {\displaystyle |A|} {\displaystyle |A|} = √ ( a 2 + b 2 + c 2 ) {\displaystyle (a^{2}+b^{2}+c^{2})} {\displaystyle (a^{2}+b^{2}+c^{2})}. For example, if a = 1 {\displaystyle a=1} a=1 and b = 2 {\displaystyle b=2} {\displaystyle b=2} and c = 3 {\displaystyle c=3} c=3, then A = 1 2 + 2 2 + 3 2 {\displaystyle A=1^{2}+2^{2}+3^{2}} {\displaystyle A=1^{2}+2^{2}+3^{2}}, and | A | {\displaystyle |A|} {\displaystyle |A|} = √ ( 1 2 + 2 2 + 3 2 ) {\displaystyle (1^{2}+2^{2}+3^{2})} {\displaystyle (1^{2}+2^{2}+3^{2})} = √ 9 {\displaystyle 9} 9 = 3 {\displaystyle 3} 3. Thus, the magnitude of vector A {\displaystyle A} A would be 3 units.
Example Problems
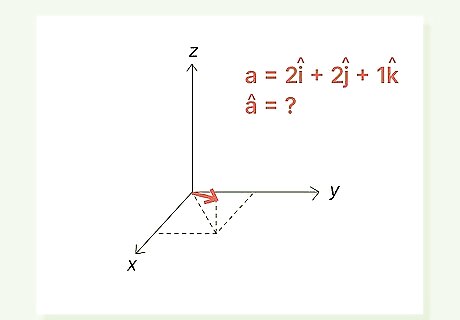
Given vector a {\displaystyle a} a = 2 i ^ {\displaystyle 2{\widehat {i}}} {\displaystyle 2{\widehat {i}}} + 2 j ^ {\displaystyle 2{\widehat {j}}} {\displaystyle 2{\widehat {j}}} + 1 k ^ {\displaystyle 1{\widehat {k}}} {\displaystyle 1{\widehat {k}}}, find a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}}.
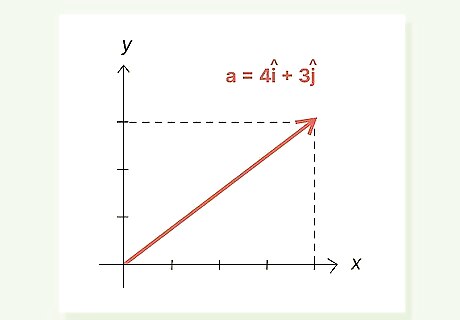
Given vector a {\displaystyle a} a = 4 i ^ {\displaystyle 4{\widehat {i}}} {\displaystyle 4{\widehat {i}}} + 3 j ^ {\displaystyle 3{\widehat {j}}} {\displaystyle 3{\widehat {j}}}, find a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}}.
Solutions
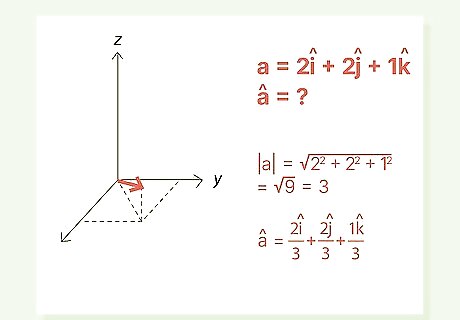
Answer #1: a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}}= 2 i ^ 3 + 2 j ^ 3 + 1 k ^ 3 {\displaystyle {\tfrac {2{\widehat {i}}}{3}}+{\tfrac {2{\widehat {j}}}{3}}+{\tfrac {1{\widehat {k}}}{3}}} {\displaystyle {\tfrac {2{\widehat {i}}}{3}}+{\tfrac {2{\widehat {j}}}{3}}+{\tfrac {1{\widehat {k}}}{3}}}. In this problem, we're asked to find the unit vector of a 3-dimensional vector; hence, the inclusion of the z-axis in the equation. To find the unit vector, we identified the magnitude of the vector and then divided the vector by its magnitude: | a | {\displaystyle |a|} {\displaystyle |a|} = √ ( 2 2 + 2 2 + 1 2 ) {\displaystyle (2^{2}+2^{2}+1^{2})} {\displaystyle (2^{2}+2^{2}+1^{2})} = 3 {\displaystyle 3} 3 a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}} = a | a | {\displaystyle {\tfrac {a}{|a|}}} {\displaystyle {\tfrac {a}{|a|}}} = 2 i ^ + 2 j ^ + 1 k ^ 3 {\displaystyle {\tfrac {2{\widehat {i}}+2{\widehat {j}}+1{\widehat {k}}}{3}}} {\displaystyle {\tfrac {2{\widehat {i}}+2{\widehat {j}}+1{\widehat {k}}}{3}}} a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}} = 2 i ^ 3 , 2 j ^ 3 , 1 k ^ 3 {\displaystyle {\tfrac {2{\widehat {i}}}{3}},{\tfrac {2{\widehat {j}}}{3}},{\tfrac {1{\widehat {k}}}{3}}} {\displaystyle {\tfrac {2{\widehat {i}}}{3}},{\tfrac {2{\widehat {j}}}{3}},{\tfrac {1{\widehat {k}}}{3}}}
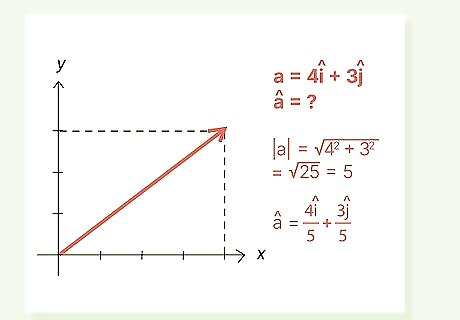
Answer #2: a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}} = 4 i ^ 5 + 3 j ^ 5 {\displaystyle {\tfrac {4{\widehat {i}}}{5}}+{\tfrac {3{\widehat {j}}}{5}}} {\displaystyle {\tfrac {4{\widehat {i}}}{5}}+{\tfrac {3{\widehat {j}}}{5}}}. For this problem, we're only asked to calculate i ^ {\displaystyle {\widehat {i}}} {\displaystyle {\widehat {i}}} and j ^ {\displaystyle {\widehat {j}}} {\displaystyle {\widehat {j}}}. Just as with the previous problem, start by calculating the magnitude using the Pythagorean Theorem. Then divide the vector by the magnitude: | a | {\displaystyle |a|} {\displaystyle |a|} = √ ( 4 2 + 3 2 ) {\displaystyle (4^{2}+3^{2})} {\displaystyle (4^{2}+3^{2})} = 5 {\displaystyle 5} 5 a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}} = a | a | {\displaystyle {\tfrac {a}{|a|}}} {\displaystyle {\tfrac {a}{|a|}}} = 4 i ^ + 3 j ^ 5 {\displaystyle {\tfrac {4{\widehat {i}}+3{\widehat {j}}}{5}}} {\displaystyle {\tfrac {4{\widehat {i}}+3{\widehat {j}}}{5}}} a ^ {\displaystyle {\widehat {a}}} {\displaystyle {\widehat {a}}} = 4 i ^ 5 + 3 j ^ 5 {\displaystyle {\tfrac {4{\widehat {i}}}{5}}+{\tfrac {3{\widehat {j}}}{5}}} {\displaystyle {\tfrac {4{\widehat {i}}}{5}}+{\tfrac {3{\widehat {j}}}{5}}}



















Comments
0 comment