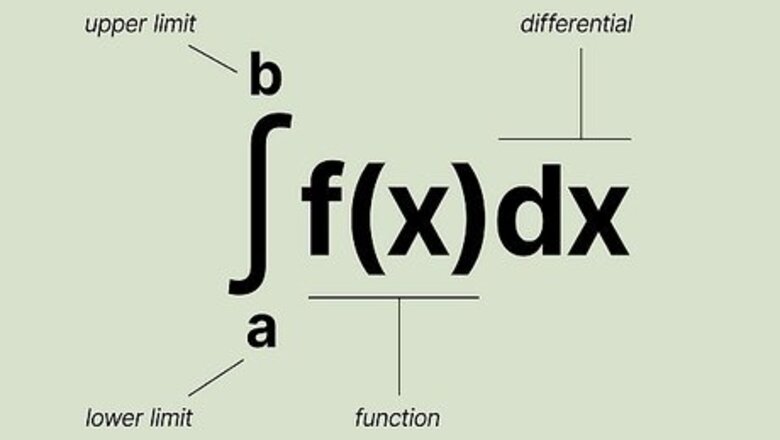
Finding the Area Under the Curve in Calculus

Cardism

Editor

posted on 2 years ago — updated on 1 second ago

29
views

While finding the area under a curve in calculus isn’t as straightforward as finding the area of various geometric shapes, it’s not as difficult as you might fear! We’re here to help you understand the question, choose the right formula, plug in the data, and calculate the result. Check out the detailed example for a step-by-step walk-through, then move onto the sample problems to help build your skills.

Things You Should Know

Plug your given function into the formula A = ∫a,b f(x) dx.
Use the power rule [∫a,b f(x) dx = (n^x+1)/(n+1) |a,b] to set up your calculation.
Utilize the fundamental theorem [∫a,b f(x) dx = F(b) - F(a)] to complete the problem and find your answer.

Summary

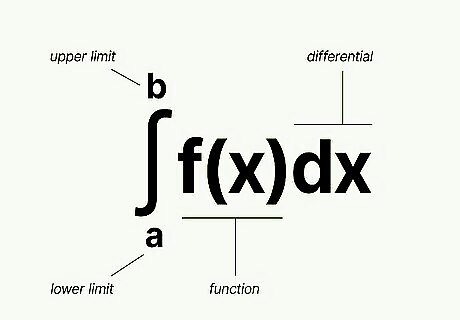
Find the area under a curve by doing a definite integral with A = ∫a,b f(x) dx. This is the standard formula you’ll use to determine the area under a curve. It tells you that you’re finding the differential (dx) of the integral (∫) of a function (f(x)). ∫a,b indicates that this is a definite (not indefinite) integral with known limits (for example, if you’re asked to find the area between x=0 and x=4).

Detailed Example

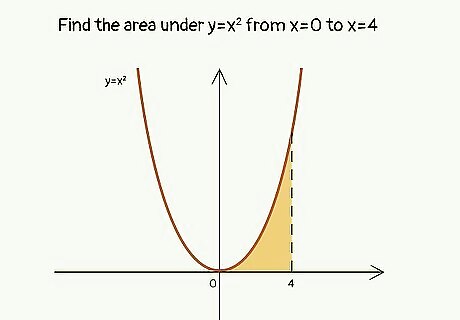
Sample Problem—Find the area under y=x^2 from x=0 to x=4. Expect the question to be phrased something along these lines. To help you visualize the curve and the area you need to determine, consider graphing the function. If you do graph it, you’ll see that y=x^2 looks like a big smiley face with its vertex (the point where the curve changes direction) at x=0, y=0. For this sample problem, you need to calculate the area (in square units) between the vertex (x=0) and an imaginary straight line drawn from x=4 along the x-axis up to the curve.

Use the formula A = ∫a,b f(x) dx to set up the definite integral. As mentioned in the “Summary” section of this article, you need to do a definite integral between two points (limits) in order to determine the area under a curve between those two points. In our example, the function (f(x)) is y=x^2, and the limits are x=0 and x=4): A = ∫a,b f(x) dx → A = ∫0,4 x^2 dx

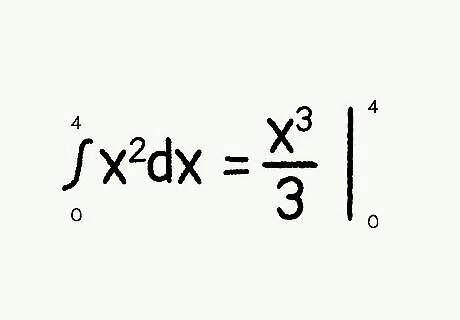
Begin the process of solving the integral. Start integrating by using the “power rule”—raising the exponent of the function by one and dividing it by that raised exponent. In this case, that means x^2 becomes (x^3)/3. Place a vertical bar afterward to designate the limits: A = (x^3)/3 |0,4

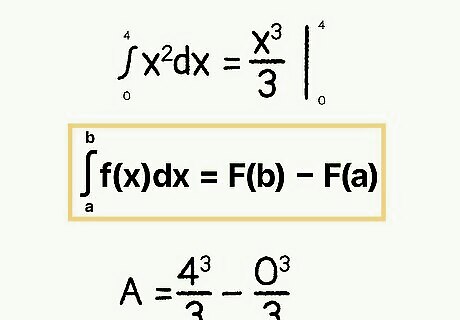
Set up your calculation with the fundamental theorem. According to the fundamental theorem of calculus, ∫a,b f(x) dx = F(b) - F(a). You get F(b) by plugging b (x=4) into (x^3)/3, and F(a) by plugging a (x=0) into the same: A = [(4^3)/3] - [(0^3)/3]

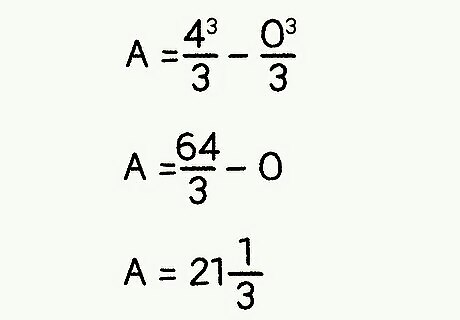
Solve for A to calculate the result. You’re in the home stretch now—just navigate some arithmetic and you’ll have the answer! Remember to label your area result as “square units” unless given a different unit of measurement. A = 64/3 - 0 A = 21 1/3 square units

Sample Problems

Find the area under y=x^3 from x=1 to x=3. A = ∫a,b f(x) dx A = ∫1,3 x^3 dx A = (x^4)/4 |1,3 A = (3^4)/4 - (1^4)/4 A = 81/4 - 1/4 = 80/4 A = 20 square units

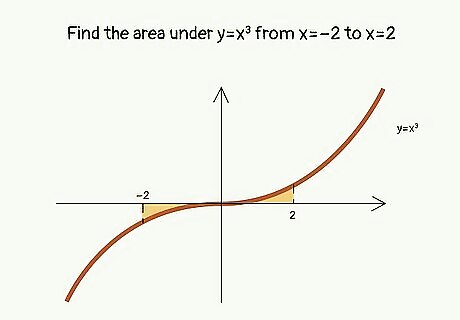
Find the area under y=x^3 from x=-2 to x=2. A = ∫a,b f(x) dx A = ∫-2,2 x^3 dx A = (x^4)/4 |-2,2 A = (2^4)/4 - (-2^4)/4 A = 16/4 - 16/4 A = 0 square units This answer may seem wrong, especially if you graph y=x^3: how can it have zero area under the curve? Mathematically speaking, any area below the x-axis is a negative area; since the areas above and below the x-axis are equal and cancel each other out, the result is A = 0.

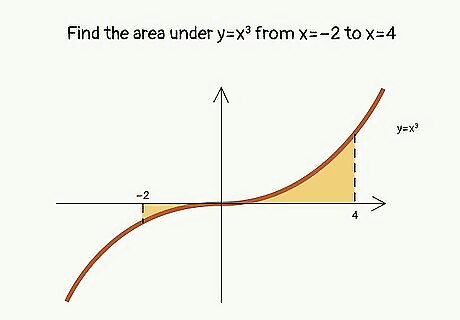
Find the area under y=x^3 from x=-2 to x=4. A = ∫a,b f(x) dx A = ∫-2,4 x^3 dx A = (x^4)/4 |-2,4 A = (4^4)/4 - (-2^4)/4 A = 256/4 - 16/4 = 240/4 A = 60 square units Like with the previous example (y=x^3 from x=-2 to x=2), remember that the area below the x-axis is actually a negative area. In this case, though, there is a greater area above the axis, leading to the final positive result.

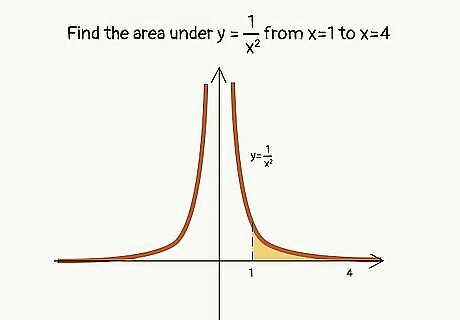
Find the area under y=1/(x^2) from x=1 to x=4. A = ∫a,b f(x) dx A = ∫1,4 1/(x^2) dx = ∫1,4 x^-2 dx A = (x^-1)/-1 |1,4 = -1/x |1,4 A = -1/4 - (-1/1) = -1/4 + 1 A = 3/4 square units

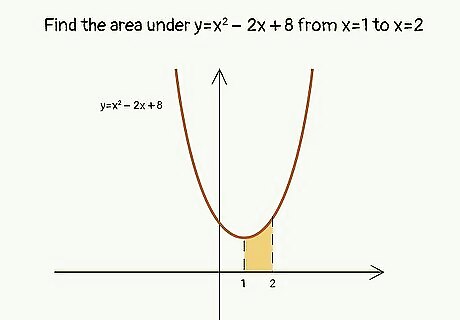
Find the area under y=x^2-2x+8 from x=1 to x=2. A = ∫a,b f(x) dx A = ∫1,2 x^2-2x+8 dx A = (x^3)/3 - (2x^2)/2 + 8x |1,2 A = (x^3)/3 - x^2 + 8x |1,2 A = [(2^3)/3 - 2^2 + 8(2)] - [(1^3)/3 - 1^2 + 8(1)] A = [8/3 - 4 + 16] - [1/3 - 1 + 8] A = 8/3 - 4 + 16 - 1/3 + 1 - 8 A = 5 + 7/3 = 7 1/3 square units

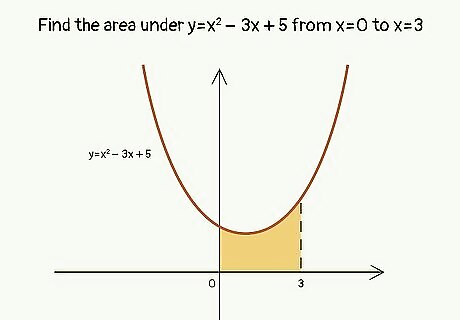
Find the area under y=x^2-3x+5 from x=0 to x=3. A = ∫a,b f(x) dx A = ∫0,3 x^2-3x+5 A = (x^3)/3 - (3x^2)/2 + 5x |0,3 A = [(3^3)/3 - (3(3^2))/2 + 5(3)] - [(0^3)/3 - (3(0^2))/2 + 5(0)] A = 27/3 - 27/2 + 15 - 0 = 24 - 27/2 A = 10 1/2 square units