Calculating Change in Momentum Using Mass & Velocity or Force & Time

• The change in momentum can be calculated using two possible formulas: Δp = m(Δv) and Δp = F(Δt).^[2]
• The formula Δp = m(Δv) tells us that the change in momentum (Δp) is equal to mass (m) multiplied by change in velocity (Δv).^[3]
• The formula Δp = F(Δt) tells us that the change in momentum (Δp) is equal to the force applied to an object (F) multiplied by the total time the force was applied (Δt).^[4]
• Use Δp = m(Δv) when you’re given mass (in kg) and velocities (in m/s). Use Δp = F(Δt) when you’re given a force (in Newtons, or “N”) and time (in seconds).

Change in Momentum Formulas

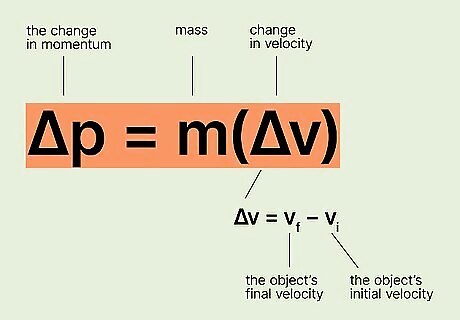
Formula #1: Δp = m(Δv) The change in momentum (Δp) is equal to mass (m) multiplied by change in velocity (Δv). Use this formula when you know the mass of an object, as well as the velocity it gained or lost. The change in momentum (Δp) is expressed in kg m/s (kilogram meters per second). The mass is expressed in kg. The change in velocity is expressed in m/s (meters per second). Δv can also be expressed as vf - vi where vf = the object’s final velocity and vi = the object’s initial (or starting) velocity. Therefore, you might see the equation Δp = m(Δv) represented as Δp = m(vf - vi).

Formula #2: Δp = F(Δt) The change in momentum (Δp) is equal to the force applied to an object (F) multiplied by the total time the force was applied (Δt). Use this formula when you know the force applied to an object, as well as how long the force was applied. The change in momentum (Δp) is expressed in kg m/s (kilogram meters per second). The force (F) is expressed in Newtons. In most cases, Newtons are abbreviated as “N”. The amount of time the force was applied (Δt) is expressed in seconds. Δt is also called the “time interval.”

How to Calculate Change in Momentum

Using Δp = m(Δv) Let’s say a 10 kg object accelerates from 10 m/s to 30 m/s. We know the mass (m) = 10 kg. To find the change in velocity (Δv), we subtract the final speed from the starting speed. Since 30 m/s - 10 m/s = 20 m/s, we know that Δv = 20 m/s. This means that Δp = 10 kg * 20 m/s. Therefore, Δp = 200 kg m/s. We knew to use the formula Δp =m(Δv) because we were provided with mass (in kg) and velocities (in m/s). Remember that the change in momentum (Δp) is always expressed in kg m/s.

Using Δp = F(Δt) Let’s say that a force of 12 Newtons is applied to an object for 45 seconds. We know that F = 12 N, and Δt = 45 s. This means that Δp = 12 N * 45 s. Therefore, Δp = 540 kg m/s. We knew to use the formula Δp = F(Δt) because we were provided with the Force (in N) and time (in seconds). The change in momentum (Δp) is always expressed in kg m/s, regardless of which formula you use.

Example Problems

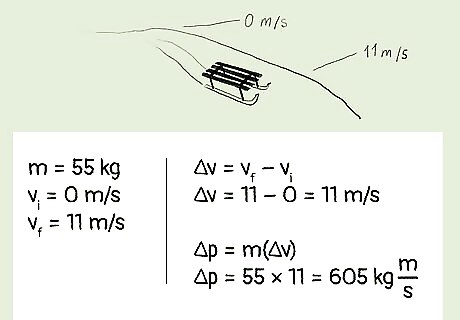
Example 1: A stationary 55 kg sled is pushed down a hill until it reaches 11 m/s. What is the change in the sled’s momentum? Which formula should you use to calculate it? Since we were provided with mass and velocity, we should use the formula Δp = m(Δv). We know that m = 55kg. Because the sled was stationary when it began moving, we know that it accelerated from 0 m/s to 11 m/s. This means that Δv = 11 m/s - 0 m/s. Therefore, Δv = 11 m/s. We can now plug in the values for m and Δv into the formula: Δp = 55 kg * 11 m/s, which equals 605 kg m/s. Therefore, the sled’s change in momentum is 605 kg m/s.

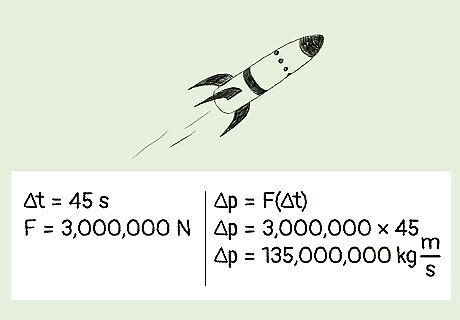
Example 2: A rocket engine ignites and burns for 45 s, applying a force of 3 million N to a spacecraft. What’s the change in the rocket’s momentum? Which formula should you use? Since we’re provided with a force and a time, we should use the formula Δp = F(Δt). We know the force was 3,000,000 N. Because the rocket engine only applies a force while it’s burning, we know that the force was applied to the spacecraft for a total of 45 of seconds. We can now plug in the values for F and Δt into the formula: Δp = 3,000,000 N * 45 s, which equals 135,000,000 kg m/s. Therefore, the change in the rocket’s momentum is 135,000,000 kg m/s (or 1.35*10^8 kg m/s).

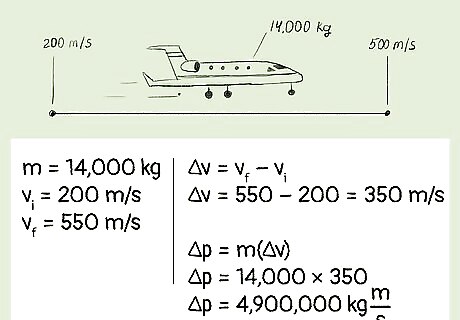
Example 3: A 14,000 kg aircraft accelerates from 200 m/s to 550 m/s. What’s the aircraft’s change in momentum? Because we have mass and velocity, we should use Δp =m(Δv). We know the mass is 14,000 kg. Because the plane accelerated from 200 m/s to 550 m/s, we know that Δv = 550 m/s - 200 m/s. Therefore, Δv = 350 m/s. In other words, the aircraft’s change in velocity is 350 m/s. Plugging in these values gives us Δp = 14,000 kg * 350 m/s, which equals 4,900,000 kg m/s. Therefore, the aircraft’s change in momentum is 4,900,000 kg m/s.

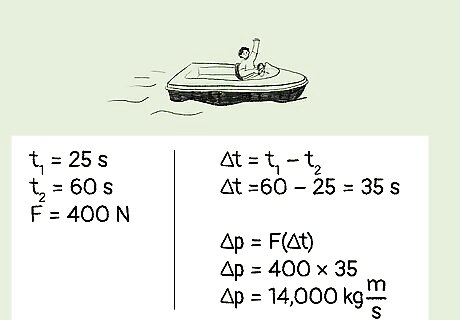
Example 4: A scientist observes a boat sitting in a lake. After 25 seconds, the boat’s engine begins applying a force of 400 N, accelerating the boat. When the engine stops, the scientist notes that they had observed the boat for a total of 60 seconds. What is the boat’s change in momentum? Because we’re provided with a force and a time, we should use the formula Δp = F(Δt). We know F = 400 N. We know that the scientist observed the boat for a total of 60 s. However, the boat’s engine did not begin applying a force until 25 s had passed. Therefore, to find the time that the force was actually applied (Δt), we need to find the difference between 60 s and 25 s. Δt = 60 s - 25 s. Therefore, Δt = 35 s. In other words, the force was applied to the boat for a total of 35 seconds. Plugging in the values for F and Δt into our formula, Δp = F(Δt), we know that Δp = 400 N * 35 s, which equals 14,000 kg m/s. Therefore, the boat’s change in momentum is 14,000 kg m/s.