Using the Correct Formula to Find the Focus of a Parabola

• Depending on the type of parabola, use the equation ${\displaystyle y=a(x-h)^{2}+k}$ or ${\displaystyle x=a(y-k)^{2}+h}$ to determine the parabola’s vertex coordinates.
• Once you have the vertex coordinates, use the formula ${\displaystyle (h,k+1/(4a))}$ or ${\displaystyle (h+1/(4a),k)}$ to calculate the graph coordinates of the focus.

What terms (like “parabola”) should I know?

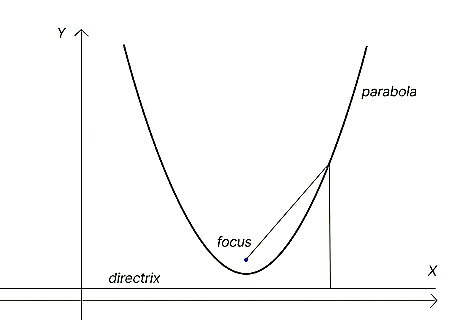
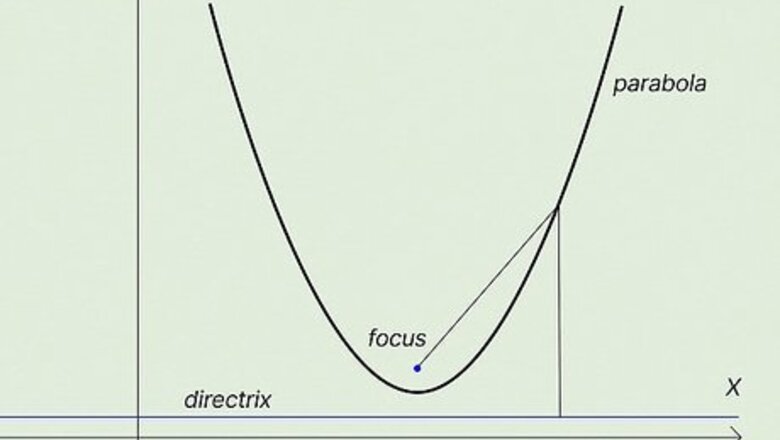
Parabola: A parabola can be defined as the graph of a quadratic equation—that is, the curved line you’ll get if you plot the equation on graph paper. Or, if you want to be more technical, it’s a curved line in which all coordinate points ( x , y ) {\displaystyle (x,y)} (x,y) along the line are equidistant from a specific focal point and a specific line called a directrix. In practical terms, it’s often easier to recognize parabolas in three dimensions. For example, think of large parabolic satellite dishes, or the clear plastic parabolic microphones you see on the sidelines of football games. Both of these direct waves (radio, sound, etc.) toward a single point—the focal point (or focus).

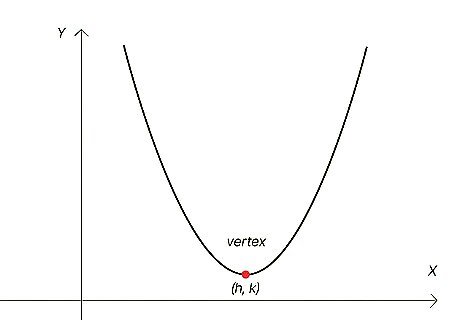
Vertex: The vertex is the “turning point” of a parabola—the point along the curve at which it changes direction. So, in a classic “U”-shaped parabola, the vertex is at the very bottom of the “U” shape. You need to know the ( x , y ) {\displaystyle (x,y)} (x,y) coordinates of the vertex in order to find the coordinates of the focus. Although they’re ( x , y ) {\displaystyle (x,y)} (x,y) coordinates, you’ll see the vertex coordinates represented by ( h , k ) {\displaystyle (h,k)} (h,k) in parabola equations and formulas.

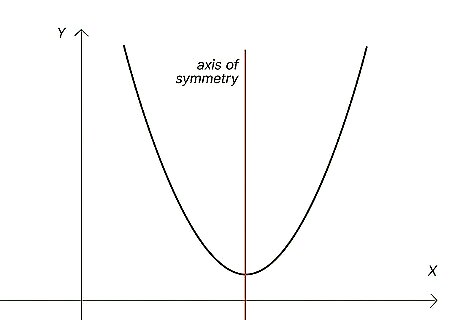
Axis of symmetry: The axis of symmetry is a line that runs through the vertex point and divides the parabola exactly in half. The parabola is a mirror image of itself on either side of the axis of symmetry. For our needs, it’s also important that the vertex is always exactly halfway between the focus and the directrix along the axis of symmetry.

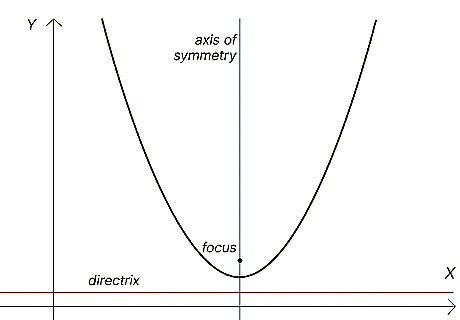
Directrix: The directrix is a straight line that crosses the axis of symmetry and is perpendicular to it. The directrix is always outside of the parabola but closest to the vertex. For example, in a classic “U” parabola, adding the directrix line makes it look like you underlined the "U." The distance between the vertex and the directrix (at the axis of symmetry) is always exactly the same as that between the vertex and the focus.

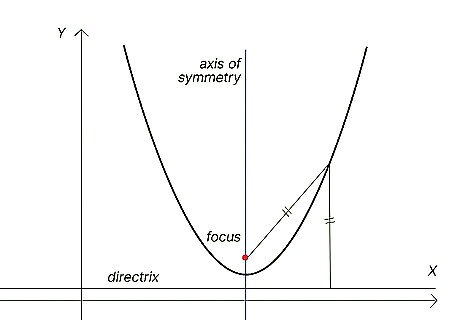
Focus: The focus is a point along the axis of symmetry, inside the parabola, that is equal in distance from the vertex as is the directrix. So, if the directrix is 2 units away from the vertex, the focus is also 2 units away (and, as a result, 4 units away from the directrix). If you draw a straight line from the focus to any point along the curve of the parabola, and then draw a straight line from that point to intersect at a right angle with the directrix, you’ll find that both of those lines are always equal in length.

Which equations/formulas do I use?

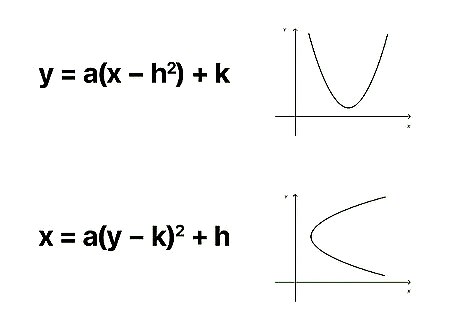
y = a ( x − h ) 2 + k {\displaystyle y=a(x-h)^{2}+k} {\displaystyle y=a(x-h)^{2}+k} or x = a ( y − k ) 2 + h {\displaystyle x=a(y-k)^{2}+h} {\displaystyle x=a(y-k)^{2}+h}. You’ll use one of these “vertex form of a parabola” equations based on the type of parabola you’re dealing with. A “regular” parabola that opens upward or downward (like a right-side up or upside-down “U”) needs to be converted into the form of the first equation, while a “sideways” parabola that opens to the side (like a forwards or backwards “C”) must be converted to the second. If you have a graph of the parabola, it’s easy to tell which equation to use. But what if you’re only given the parabola in equation form? Here’s the trick to use: If the x {\displaystyle x} x component is squared in the parabola’s equation—for example y = x 2 {\displaystyle y=x^{2}} y=x^{2}—convert it into the form y = a ( x − h ) 2 + k {\displaystyle y=a(x-h)^{2}+k} {\displaystyle y=a(x-h)^{2}+k}. If the y {\displaystyle y} y component is squared (like in x = y 2 {\displaystyle x=y^{2}} {\displaystyle x=y^{2}}), use x = a ( y − k ) 2 + h {\displaystyle x=a(y-k)^{2}+h} {\displaystyle x=a(y-k)^{2}+h}. In both equations, ( h , k ) {\displaystyle (h,k)} (h,k) represent the coordinates of the parabola’s vertex, and a {\displaystyle a} a represents its slope.

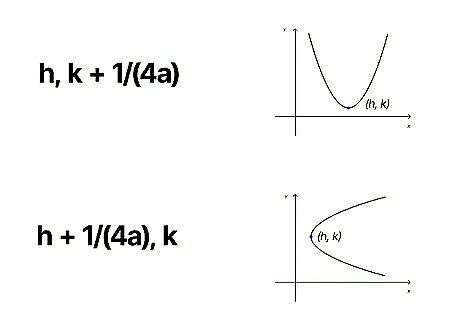
( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))} or ( h + 1 / ( 4 a ) , k ) {\displaystyle (h+1/(4a),k)} {\displaystyle (h+1/(4a),k)}. Once you have determined (or have been given) the coordinates of the parabola’s vertex, you’ll use one of these formulas to determine the coordinates of the focus. Here’s how to know which to use: Use ( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))} for a “regular” parabola in form y = a ( x − h 2 ) + k {\displaystyle y=a(x-h^{2})+k} {\displaystyle y=a(x-h^{2})+k}. Use ( h + 1 / ( 4 a ) , k ) {\displaystyle (h+1/(4a),k)} {\displaystyle (h+1/(4a),k)} for a “sideways” parabola in form x = a ( y − k ) 2 + h {\displaystyle x=a(y-k)^{2}+h} {\displaystyle x=a(y-k)^{2}+h}.

Example Walk-Through: y=x^2

Put the equation into the vertex form of a parabola. Because the x {\displaystyle x} x portion of the equation is squared, the correct vertex form is y = a ( x − h ) 2 + k {\displaystyle y=a(x-h)^{2}+k} {\displaystyle y=a(x-h)^{2}+k}, meaning this is a “regular” parabola (it opens either up or down). y = x 2 {\displaystyle y=x^{2}} y=x^{2} → y = 1 ( x − 0 ) 2 + 0 {\displaystyle y=1(x-0)^{2}+0} {\displaystyle y=1(x-0)^{2}+0} Also note that, because a {\displaystyle a} a is positive, the parabola opens upward.

Identify the vertex and the focus equation. In y = 1 ( x − 0 ) 2 + 0 {\displaystyle y=1(x-0)^{2}+0} {\displaystyle y=1(x-0)^{2}+0}, both h {\displaystyle h} h and k {\displaystyle k} k equal zero ( 0 , 0 ) {\displaystyle (0,0)} (0,0). That means the focus equation is ( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))} → ( 0 , 0 + 1 / ( 4 a ) ) {\displaystyle (0,0+1/(4a))} {\displaystyle (0,0+1/(4a))}

Solve for a {\displaystyle a} a to find the focus coordinates. a = 1 {\displaystyle a=1} a=1 in y = 1 ( x − 0 ) 2 + 0 {\displaystyle y=1(x-0)^{2}+0} {\displaystyle y=1(x-0)^{2}+0} So, the focus equation is ( 0 , 0 + 1 / ( 4 ( 1 ) ) ) {\displaystyle (0,0+1/(4(1)))} {\displaystyle (0,0+1/(4(1)))} Therefore, the focus of y = x 2 {\displaystyle y=x^{2}} y=x^{2} is at ( 0 , 1 / 4 ) {\displaystyle (0,1/4)} {\displaystyle (0,1/4)}

More Examples

Find the focus of the parabola x = y 2 {\displaystyle x=y^{2}} {\displaystyle x=y^{2}}. This is a “sideways” parabola because the y {\displaystyle y} y component is squared, so use the vertex form x = a ( y − k ) 2 + h {\displaystyle x=a(y-k)^{2}+h} {\displaystyle x=a(y-k)^{2}+h} and the focus equation ( h + 1 / ( 4 a ) , k ) {\displaystyle (h+1/(4a),k)} {\displaystyle (h+1/(4a),k)}. x = y 2 {\displaystyle x=y^{2}} {\displaystyle x=y^{2}} → x = 1 ( y − 0 ) 2 + 0 {\displaystyle x=1(y-0)^{2}+0} {\displaystyle x=1(y-0)^{2}+0} Vertex ( h , k ) = ( 0 , 0 ) {\displaystyle (h,k)=(0,0)} {\displaystyle (h,k)=(0,0)}, a = 1 {\displaystyle a=1} a=1 ( h + 1 / ( 4 a ) , k ) {\displaystyle (h+1/(4a),k)} {\displaystyle (h+1/(4a),k)} → ( 0 + 1 / ( 4 ( 1 ) ) , 0 ) {\displaystyle (0+1/(4(1)),0)} {\displaystyle (0+1/(4(1)),0)} → ( 1 / 4 , 0 ) {\displaystyle (1/4,0)} {\displaystyle (1/4,0)} Answer: The focus is located at ( 1 / 4 , 0 ) {\displaystyle (1/4,0)} {\displaystyle (1/4,0)}.

Find the focus of the parabola ( y − 3 ) 2 = 8 ( x − 5 ) {\displaystyle (y-3)^{2}=8(x-5)} {\displaystyle (y-3)^{2}=8(x-5)}. Here’s another “sideways” parabola because the y component is squared, so use the vertex form x = a ( y − k ) 2 + h {\displaystyle x=a(y-k)^{2}+h} {\displaystyle x=a(y-k)^{2}+h} and the focus equation ( h + 1 / ( 4 a ) , k ) {\displaystyle (h+1/(4a),k)} {\displaystyle (h+1/(4a),k)}. Put ( y − 3 ) 2 = 8 ( x − 5 ) {\displaystyle (y-3)^{2}=8(x-5)} {\displaystyle (y-3)^{2}=8(x-5)} in x = a ( y − k ) 2 + h {\displaystyle x=a(y-k)^{2}+h} {\displaystyle x=a(y-k)^{2}+h} form: ( x − 5 ) = 1 / 8 ( y − 3 ) 2 ) {\displaystyle (x-5)=1/8(y-3)^{2})} {\displaystyle (x-5)=1/8(y-3)^{2})} → x = 1 / 8 ( y − 3 ) 2 + 5 {\displaystyle x=1/8(y-3)^{2}+5} {\displaystyle x=1/8(y-3)^{2}+5} Vertex ( h , k ) = ( 5 , 3 ) {\displaystyle (h,k)=(5,3)} {\displaystyle (h,k)=(5,3)}, a = 1 / 8 {\displaystyle a=1/8} {\displaystyle a=1/8} ( h + 1 / ( 4 a ) , k ) {\displaystyle (h+1/(4a),k)} {\displaystyle (h+1/(4a),k)} → ( 5 + 1 / ( 4 ( 1 / 8 ) ) , 3 ) {\displaystyle (5+1/(4(1/8)),3)} {\displaystyle (5+1/(4(1/8)),3)} ( 5 + 1 / ( 1 / 2 ) , 3 ) {\displaystyle (5+1/(1/2),3)} {\displaystyle (5+1/(1/2),3)} → ( 5 + 2 , 3 ) {\displaystyle (5+2,3)} {\displaystyle (5+2,3)} Answer: The focus is located at ( 7 , 3 ) {\displaystyle (7,3)} {\displaystyle (7,3)}.

Find the focus of the parabola ( x + 3 ) 2 = − 20 ( y − 1 ) {\displaystyle (x+3)^{2}=-20(y-1)} {\displaystyle (x+3)^{2}=-20(y-1)}. This one’s a “regular” parabola (the x {\displaystyle x} x component is squared), so use y = a ( x − h ) 2 + k {\displaystyle y=a(x-h)^{2}+k} {\displaystyle y=a(x-h)^{2}+k} and ( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))}. Put ( x + 3 ) 2 = − 20 ( y − 1 ) {\displaystyle (x+3)^{2}=-20(y-1)} {\displaystyle (x+3)^{2}=-20(y-1)} in the proper form: ( y − 1 ) = − 1 / 20 ( x + 3 ) 2 {\displaystyle (y-1)=-1/20(x+3)^{2}} {\displaystyle (y-1)=-1/20(x+3)^{2}} → y = − 1 / 20 ( x + 3 ) 2 + 1 {\displaystyle y=-1/20(x+3)^{2}+1} {\displaystyle y=-1/20(x+3)^{2}+1} Vertex ( h , k ) = ( − 3 , 1 ) {\displaystyle (h,k)=(-3,1)} {\displaystyle (h,k)=(-3,1)}, a = − 1 / 20 {\displaystyle a=-1/20} {\displaystyle a=-1/20} ( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))} → ( − 3 , 1 + 1 / ( 4 ( − 1 / 20 ) ) ) {\displaystyle (-3,1+1/(4(-1/20)))} {\displaystyle (-3,1+1/(4(-1/20)))} ( − 3 , 1 + 1 / ( − 1 / 5 ) {\displaystyle (-3,1+1/(-1/5)} {\displaystyle (-3,1+1/(-1/5)} → ( − 3 , 1 + ( − 5 ) ) {\displaystyle (-3,1+(-5))} {\displaystyle (-3,1+(-5))} Answer: The focus is located at ( − 3 , − 4 ) {\displaystyle (-3,-4)} {\displaystyle (-3,-4)}

Find the focus of the parabola ( x − 7 ) 2 = 3 ( y − 4 ) {\displaystyle (x-7)^{2}=3(y-4)} {\displaystyle (x-7)^{2}=3(y-4)}. It’s another “regular” parabola, which means you use y = a ( x − h ) 2 + k {\displaystyle y=a(x-h)^{2}+k} {\displaystyle y=a(x-h)^{2}+k} and ( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))}. Put ( x − 7 ) 2 = 3 ( y − 4 ) {\displaystyle (x-7)^{2}=3(y-4)} {\displaystyle (x-7)^{2}=3(y-4)} in the proper form: ( y − 4 ) = 1 / 3 ( x − 7 ) 2 {\displaystyle (y-4)=1/3(x-7)^{2}} {\displaystyle (y-4)=1/3(x-7)^{2}} → y = 1 / 3 ( x − 7 ) 2 + 4 {\displaystyle y=1/3(x-7)^{2}+4} {\displaystyle y=1/3(x-7)^{2}+4} Vertex ( h , k ) = ( 7 , 4 ) {\displaystyle (h,k)=(7,4)} {\displaystyle (h,k)=(7,4)}, a = 1 / 3 {\displaystyle a=1/3} {\displaystyle a=1/3} ( h , k + 1 / ( 4 a ) ) {\displaystyle (h,k+1/(4a))} {\displaystyle (h,k+1/(4a))} → ( 7 , 4 + 1 / ( 4 ( 1 / 3 ) ) ) {\displaystyle (7,4+1/(4(1/3)))} {\displaystyle (7,4+1/(4(1/3)))} ( 7 , 4 + 1 / ( 4 / 3 ) ) {\displaystyle (7,4+1/(4/3))} {\displaystyle (7,4+1/(4/3))} → ( 7 , 4 + ( 3 / 4 ) ) {\displaystyle (7,4+(3/4))} {\displaystyle (7,4+(3/4))} → ( 7 , ( 16 / 4 ) + ( 3 / 4 ) ) {\displaystyle (7,(16/4)+(3/4))} {\displaystyle (7,(16/4)+(3/4))} Answer: the focus is located at ( 7 , 19 / 4 ) {\displaystyle (7,19/4)} {\displaystyle (7,19/4)}