views
Finding the Sides of a Right Triangle
Ensure that your triangle is a right triangle. The Pythagorean Theorem is applicable only to right triangles, so, before proceeding, it's important to make sure your triangle fits the definition of a right triangle. Luckily, there is only one qualifying factor - to be a right triangle, your triangle must contain one angle of exactly 90 degrees. As a form of visual shorthand, right angles are often marked with a small square, rather than a rounded "curve", to identify them as such. Look for this special mark in one of the corners of your triangle.
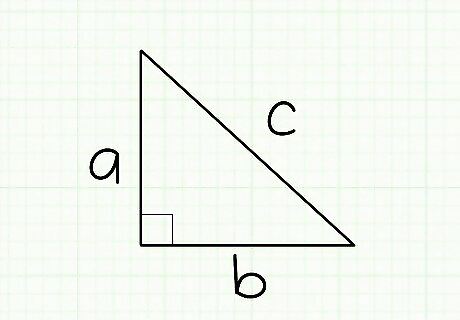
Assign the variables a, b, and c to the sides of your triangle. In the Pythagorean Theorem, the variables a and b refer to the sides that meet in a right angle, while the variable c refers to the hypotenuse - the longest side which is always opposite the right angle. So, to begin, assign the shorter sides of your triangle the variables a and b (it doesn't matter which side is labeled 'a' or 'b'), and assign the hypotenuse the variable c.
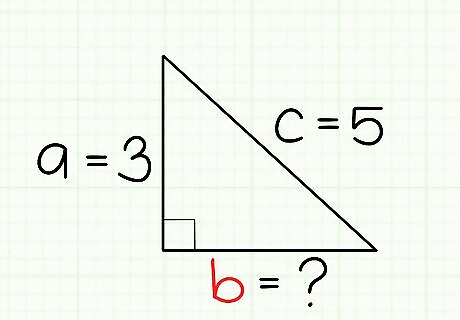
Determine which side(s) of the triangle you are solving for. The Pythagorean Theorem allows mathematicians to find the length of any one of a right triangle's sides as long as they know the lengths of the other two sides. Determine which of your sides has an unknown length - a, b, and/or c. If the length of only one of your sides is unknown, you're ready to proceed. Let's say, for example, that we know that our hypotenuse has a length of 5 and one of the other sides has a length of 3, but we're not sure what the length of the third side is. In this case, we know we're solving for the length of the third side, and, because we know the lengths of the other two, we're ready to go! We'll return to this example problem in the following steps. If the lengths of two of your sides are unknown, you'll need to determine the length of one more side to use the Pythagorean Theorem. Basic trigonometry functions can help you here if you know one of the non-right angles in the triangle.
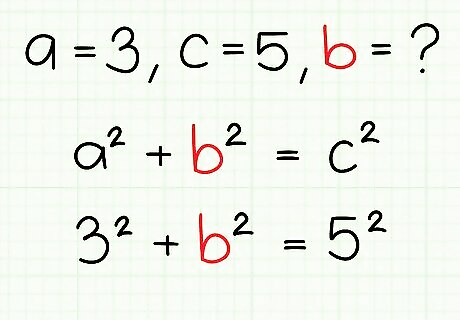
Plug your two known values into the equation. Insert your values for the lengths of the sides of your triangle into the equation a + b = c. Remember that a and b are the non hypotenuse sides, while c is the hypotenuse. In our example, we know the length of one side and the hypotenuse (3 & 5), so we would write our equation as 3² + b² = 5²
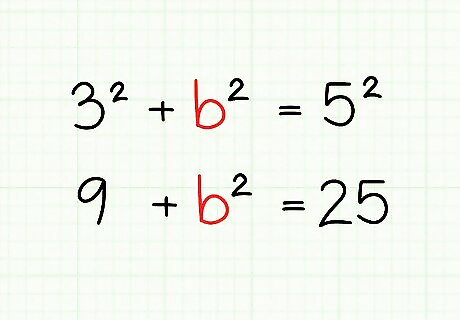
Calculate the squares. To solve your equation, begin by taking the square of each of your known sides. Alternatively, if you find it easier, you may leave your side lengths in the exponent form, then square them later. In our example, we would square 3 and 5 to get 9 and 25, respectively. We can rewrite our equation as 9 + b² = 25.
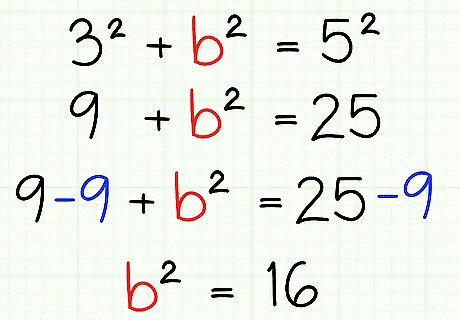
Isolate your unknown variable on one side of the equals sign. If necessary, use basic algebra operations to get your unknown variable on one side of the equals sign and your two squares on the other side of the equals sign. If you're solving for the hypotenuse, c will already be isolated, so you won't need to do anything to isolate it. In our example, our current equation is 9 + b² = 25. To isolate b², let's subtract 9 from both sides of the equation. This leaves us with b² = 16. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To solve an equation for a variable like "x," you need to manipulate the equation to isolate x. Use techniques like the distributive property, combining like terms, factoring, adding or subtracting the same number, and multiplying or dividing by the same non-zero number to isolate "x" and find the answer.
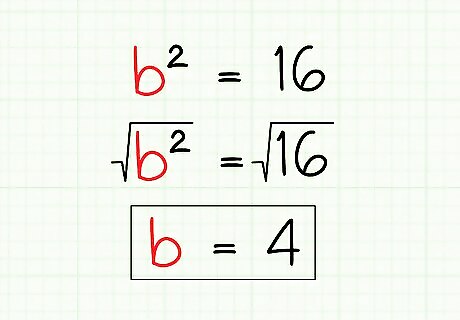
Take the square root of both sides of the equation. You should now be left with one variable squared on one side of the equation and a number on the other side. Simply take the square root of both sides to find the length of your unknown side. In our example, b² = 16, taking the square root of both sides gives us b = 4. Thus, we can say that the length of the unknown side of our triangle is 4.
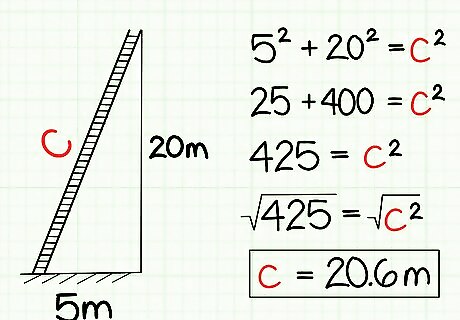
Use the Pythagorean Theorem to find the sides of real-world right triangles. The reason that the Pythagorean Theorem is so widely used today is that it's applicable in countless practical situations. Learn to recognize right triangles in real life - in any situation where two straight objects or lines meet at a right angle and a third line or object stretches diagonally across from the right angle, you can use the Pythagorean Theorem to find the length of one of the sides, given the length of the other two. Let's try real-world example that's a little more difficult. A ladder is leaning against a building. The base of the ladder is 5 meters (16.4 ft) from the bottom of the wall. The ladder reaches 20 meters (65.6 ft) up the wall of the building. How long is the ladder? "5 meters (16.4 ft) from the bottom of wall” and "20 meters (65.6 ft) up the wall” clue us into the lengths of the sides of our triangle. Since the wall and the ground (presumably) meet at a right angle and the ladder leans diagonally against the wall, we can think of this arrangement as a right triangle with sides of length a = 5 and b = 20. The length of the ladder is the hypotenuse, so c is our unknown. Let's use the Pythagorean Theorem: a² + b² = c² (5)² + (20)² = c² 25 + 400 = c² 425 = c² sqrt(425) = c c = 20.6 . The approximate length of the ladder is 20.6 meters (67.6 ft).
Calculating the Distance Between Two Points in an X-Y Plane
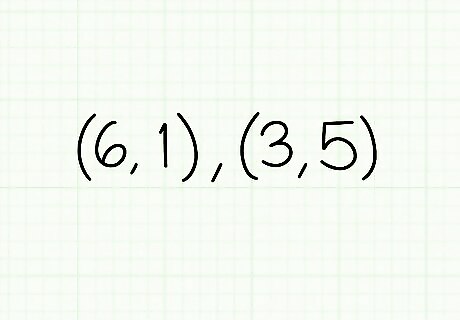
Define two points in the X-Y plane. The Pythagorean Theorem can easily be used to calculate the straight-line distance between two points in the X-Y plane. All you need to know are the x and y coordinates of any two points. Usually, these coordinates are written as ordered pairs in the form (x, y). To find the distance between these two points, we will treat each point as one of the non-right angle corners of a right triangle. By doing this, it's easy to find the length of the a and b sides, then calculate c, the hypotenuse, which is the distance between the two points.
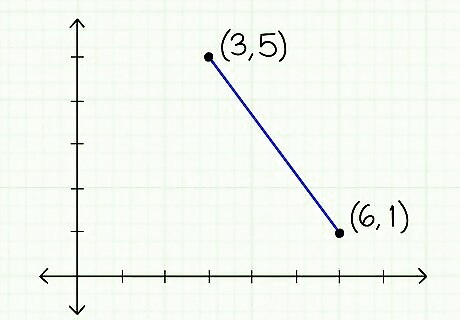
Plot your two points on a graph. In a typical X-Y plane, for each point (x,y), x gives a coordinate on the horizontal axis and y gives a coordinate on the vertical axis. You can find the distance between the two points without plotting them on a graph, but doing so gives you a visual reference that you can use to ensure your answer makes sense.
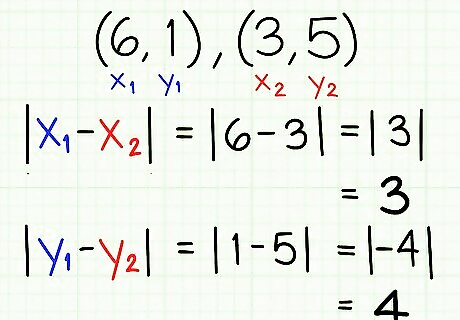
Find the lengths of the non-hypotenuse sides of your triangle. Using your two points as the corners of the triangle adjacent to the hypotenuse, find the lengths of the a and b sides of the triangle. You can do this visually on the graph, or by using the formulas |x1 - x2| for the horizontal side and |y1 - y2| for the vertical side, where (x1,y1) is your first point and (x2,y2) is your second. Let's say our two points are (6,1) and (3,5). The side length of the horizontal side of our triangle is: |x1 - x2| |3 - 6| | -3 | = 3 The length of the vertical side is: |y1 - y2| |1 - 5| | -4 | = 4 So, we can say that in our right triangle, side a = 3 and side b = 4.

Use the Pythagorean Theorem to solve for the hypotenuse. The distance between your two points is the hypotenuse of the triangle whose two sides you've just defined. Use the Pythagorean Theorem as you normally would to find the hypotenuse, setting a as the length of your first side and b as the length of the second. In our example using points (3,5) and (6,1), our side lengths are 3 and 4, so we would find the hypotenuse as follows: (3)²+(4)²= c² c= sqrt(9+16) c= sqrt(25) c= 5. The distance between (3,5) and (6,1) is 5.
Solving Pythagorean Theorem Questions
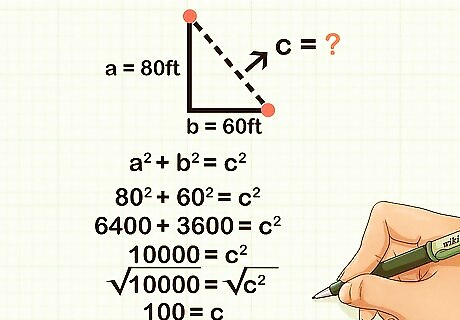
Find the shortest distance between two points. For instance, Luis walks through a park. He starts at the fountain and walks 80 feet south and 60 feet west. What is the shortest distance back to the fountain? The shortest distance between two points is a straight line. This straight line creates a hypotenuse of a right triangle, with one side 80 feet long and the other side 60 feet long. The formula for Pythagoras's theorem is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{2}+b^{2}=c^{2}, where c {\displaystyle c} c equals the length of the hypotenuse, and a {\displaystyle a} a and b {\displaystyle b} b equal the lengths of the other two sides. Since you know the lengths of the two sides, plug the values of a {\displaystyle a} a and b {\displaystyle b} b into the formula: 80 2 + 60 2 = c 2 {\displaystyle 80^{2}+60^{2}=c^{2}} 80^{2}+60^{2}=c^{2}. Square the lengths of the sides: 6400 + 3600 = c 2 {\displaystyle 6400+3600=c^{2}} 6400+3600=c^{2}. Add the squared side lengths: 10 , 000 = c 2 {\displaystyle 10,000=c^{2}} 10,000=c^{2}. Find the square root of both sides of the equation: 10 , 000 = c 2 {\displaystyle {\sqrt {10,000}}={\sqrt {c^{2}}}} {\sqrt {10,000}}={\sqrt {c^{2}}} 100 = c {\displaystyle 100=c} 100=c. The length of hypotenuse, and the shortest distance back to the fountain, is 100 ft.
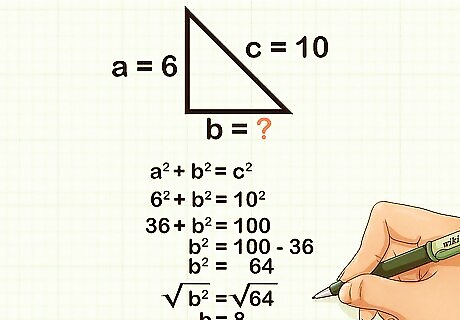
Find a missing length. For instance, find the length of x {\displaystyle x} x, given a right triangle with a hypotenuse measuring 10 cm and one side measuring 6 cm. The formula for Pythagoras's theorem is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{2}+b^{2}=c^{2}, where c {\displaystyle c} c equals the length of the hypotenuse, and a {\displaystyle a} a and b {\displaystyle b} b equal the lengths of the other two sides. Since you know the lengths of the hypotenuse and one side, plug the values of a {\displaystyle a} a and c {\displaystyle c} c into the formula: 6 2 + b 2 = 10 2 {\displaystyle 6^{2}+b^{2}=10^{2}} 6^{2}+b^{2}=10^{2}. Square the known measurements: 36 + b 2 = 100 {\displaystyle 36+b^{2}=100} 36+b^{2}=100. Subtract the squared value of a {\displaystyle a} a from both sides of the equation: b 2 = 64 {\displaystyle b^{2}=64} b^2 = 64. Find the square root of both sides of the equation: b 2 = 64 {\displaystyle {\sqrt {b^{2}}}={\sqrt {64}}} {\sqrt {b^{2}}}={\sqrt {64}} b = 8 {\displaystyle b=8} b = 8 The length of x {\displaystyle x} x is 8 cm.

Identify a right triangle. For instance, determine whether the triangle is right, given side lengths of 9, 12, and 15 cm. The formula for Pythagoras's theorem is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{2}+b^{2}=c^{2}, where c {\displaystyle c} c equals the length of the hypotenuse, and a {\displaystyle a} a and b {\displaystyle b} b equal the lengths of the other two sides. The longest side length is the potential hypotenuse. Plug this value in for c {\displaystyle c} c: a 2 + b 2 = 15 2 {\displaystyle a^{2}+b^{2}=15^{2}} a^{2}+b^{2}=15^{2}. Plug the values of the other two sides into the equation: 9 2 + 12 2 = 15 2 {\displaystyle 9^{2}+12^{2}=15^{2}} 9^{2}+12^{2}=15^{2}. Square all of the numbers: 81 + 144 = 225 {\displaystyle 81+144=225} 81+144=225. Add the square of the two sides: 225 = 225 {\displaystyle 225=225} 225=225. Since the equation is true, the triangle is right.
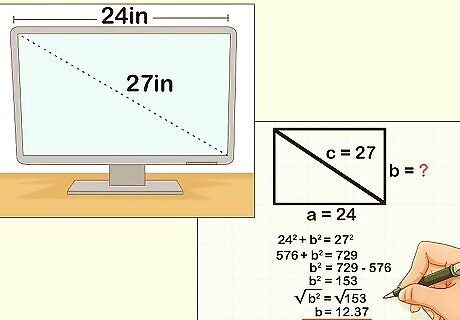
Use the diagonal of a rectangle as the hypotenuse of a right triangle. For instance, Sherrie is buying a new computer screen. It needs to be less than 12 inches high to be able to fit under the shelf over her desk. She finds a computer screen with a 27-inch diagonal, and a width of 24 inches. Will this screen fit on her desk? The formula for Pythagoras's theorem is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{2}+b^{2}=c^{2}, where c {\displaystyle c} c equals the length of the hypotenuse, and a {\displaystyle a} a and b {\displaystyle b} b equal the lengths of the other two sides. Since you know the width and the diagonal of the rectangle, plug the values of a {\displaystyle a} a and c {\displaystyle c} c into the formula: 24 2 + b 2 = 27 2 {\displaystyle 24^{2}+b^{2}=27^{2}} 24^{2}+b^{2}=27^{2}. Square the known measurements: 576 + b 2 = 729 {\displaystyle 576+b^{2}=729} 576+b^{2}=729. Subtract the squared value of a {\displaystyle a} a from both sides of the equation: b 2 = 153 {\displaystyle b^{2}=153} b^{2}=153. Find the square root of both sides of the equation: b 2 = 153 {\displaystyle {\sqrt {b^{2}}}={\sqrt {153}}} {\sqrt {b^{2}}}={\sqrt {153}} b = 12.37 {\displaystyle b=12.37} b=12.37 The height of the computer screen is about 12.37 inches. Sherrie only has room for a screen that is 12 inches high, so this screen will not fit on her desk.




















Comments
0 comment