views
When a plane region, lying entirely on one side of a fixed line in its plane, is revolved about that line, it generates a solid of revolution. The fixed line is called the axis of the solid of revolution.
As an illustration, if the region bounded by a semicircle and its diameter is revolved about that diameter, it sweeps out a spherical solid. If the region inside a right triangle is revolved about one of its legs, it generates a conical solid. When a circular disk is revolved about a line in its plane which does not intersect the disk, it sweeps out a torus (or donut).
All plane sections of a solid of revolution that are perpendicular to its axis are circular disks or regions bounded by two concentric circles.
We seek the volume of a solid of revolution. But first we must define what is meant by the "volume" of a solid of revolution.
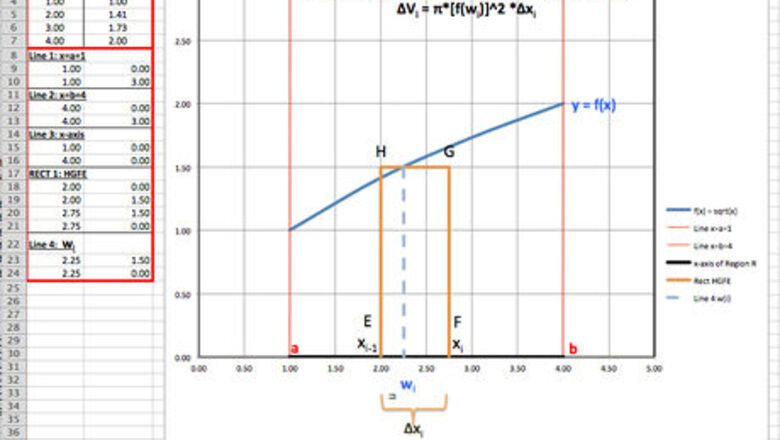
Just as in any discussion of a plane area in which it is assumed that the area of a rectangle is a product of its length and width, we start out investigation of volumes of solids of revolutions by assuming that the volume of a right circular cylinder is πr^2h (π=pi, r=radius, ^2=squared and h=height or altitude).
Start by opening a new workbook in Excel from the desktop, from the dock, or from within your Applications folder inside the Microsoft folder. Double click on Excel (either the green X on the dock or the app title in the folder) and select File New Workbook.
In Preferences, set R1C1 to unchecked or Off, set Ribbon to checked or On and set Show Formula Bar to checked or On.
Click in the far upper left top corner above the 1 of row 1 and to the left of column A. Doing so will select the entire worksheet. Format Cells Number Number to decimal places 2, show comma. Format Cells Alignment Center. # Title the first worksheet, "Rotate Function f(x)" and save the workbook as "Rotate Curves About An Axis" into an appropriate folder such as 'Microsoft Excel Imagery' or 'wikiHow Articles'.
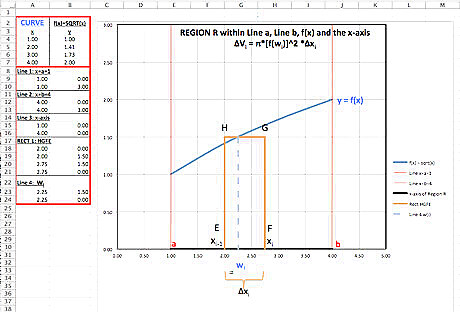
Enter to cell A1 the following text and then set Format Cell Alignment to Wrap Text: Let f be a function which is continuous on the closed interval [a,b], with f(x) ≥ 0 for a ≤ x ≤ b. You want to define the volume of the solid of revolution generated by revolving about the x-axis the region R which is bounded by the curve y = f(x), the x-axis, and the vertical lines x = a and x = b. Let f(x) = sqrt(x) and a = 1 and b = 4. Subdivide the interval [a,b] into n subintervals by a partition P, and choose n points wi, one in each subinterval. Draw n approximating rectangles with base [xi-1,xi] and altitude f(wi), i = 1, 2, 3, ... , n; a typical one of these rectangles is shown in the diagram as Rect HGFE. Revolve the region R about the x-axis to generate a solid of revolution, using the n rectangles to sweep out n right circular cylinders. The cylinders swept out by the typical rectangle, eg. Rect HGFE, is shown in the following Diagram; since the radius of its base is f(wi) and its altitude is ∆xi, its volume is ∆Vi = π*[f(wi)]^2 *∆xi. Note that if you want to create a washer type of form, the formula changes to π * ∫a [f(x)^2 = g(x)^2]*dx -- so it is a definite integral of the difference of the squares of the external function, f(x), and the internal (hole) function, g(x). Note also that you may let f be a continuous function on [a.b] and if the region bounded by y = f(x), the x-axis, and the lines x = a and x = b lies in the first quadrant, the volume of the solid of revolution generated by revolving this region about the y-axis is V = 2π * ∫a x*f(x)*dx, another definite integral.

















Comments
0 comment