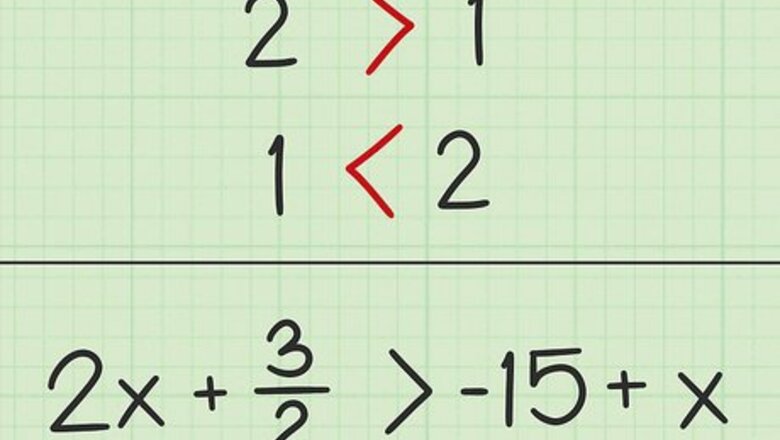
views
Solving Linear Inequalities
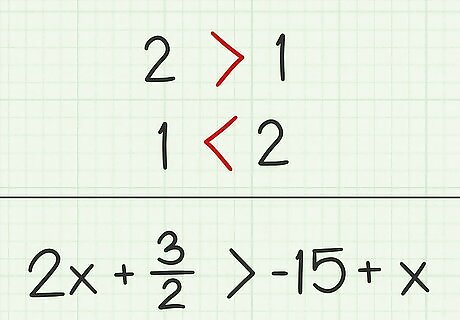
Understand the inequality signs. An inequality is like an equation, except instead of saying that the two values are equal, an inequality shows a “greater than” or “less than” relationship. The > {\displaystyle >} > sign means “greater than.” The < {\displaystyle <} means “less than.” For example, 2 x + 3 2 > − 15 + x {\displaystyle 2x+{\frac {3}{2}}>-15+x} 2x+{\frac {3}{2}}>-15+x means that the value on the left side of the inequality is greater than the value on the right side.
Combine like terms, or otherwise simplify the inequality. You can solve inequalities using the same algebraic principles you would use to solve an equation. You might need to combine variables, multiply to cancel out fractions, or use other operations to make the numbers easier to work with. Remember that you need to keep the inequality balanced, so whatever operation you perform on one side of the inequality, you must also perform on the other side. For example, if solving the inequality 2 x + 3 2 > − 15 + x {\displaystyle 2x+{\frac {3}{2}}>-15+x} 2x+{\frac {3}{2}}>-15+x, you would first multiply each part by 2 to cancel out the fraction: 2 ( 2 x + 3 2 ) > 2 ( − 15 + x ) {\displaystyle 2(2x+{\frac {3}{2}})>2(-15+x)} 2(2x+{\frac {3}{2}})>2(-15+x) 4 x + 3 > − 30 + 2 x {\displaystyle 4x+3>-30+2x} 4x+3>-30+2x
Move the variable to one side of the inequality. To do this, add or subtract variables from one side of the inequality. Remember that whatever you do to one side, you must also do to the other side. For example, in the inequality 4 x + 3 > − 30 + 2 x {\displaystyle 4x+3>-30+2x} 4x+3>-30+2x, to move the variable to one side, you would subtract 2 x {\displaystyle 2x} 2x from both sides of the inequality: 4 x + 3 > − 30 + 2 x {\displaystyle 4x+3>-30+2x} 4x+3>-30+2x 4 x + 3 − 2 x > − 30 + 2 x − 2 x {\displaystyle 4x+3-2x>-30+2x-2x} 4x+3-2x>-30+2x-2x 2 x + 3 > − 30 {\displaystyle 2x+3>-30} 2x+3>-30
Isolate the variable. In order to solve the inequality, the variable should be on one side, without coefficients or constants. Divide to cancel out coefficients, and add or subtract to remove constants. Once you have isolated the variable, you have solved the inequality. For example, in the inequality 2 x + 3 > − 30 {\displaystyle 2x+3>-30} 2x+3>-30, to isolate the x {\displaystyle x} x you need to subtract 3 from both sides, then divide both sides by 2: 2 x + 3 − 3 > − 30 − 3 {\displaystyle 2x+3-3>-30-3} 2x+3-3>-30-3 2 x > − 33 {\displaystyle 2x>-33} 2x>-33 2 x 2 > − 33 2 {\displaystyle {\frac {2x}{2}}>{\frac {-33}{2}}} {\frac {2x}{2}}>{\frac {-33}{2}} x > − 16 1 2 {\displaystyle x>-16{\frac {1}{2}}} x>-16{\frac {1}{2}} You can use interval notations to represent the solution to this inequality. For this example, it would be given as ( − 16 1 2 , ∞ ) {\displaystyle \left(-16{\frac {1}{2}},\infty \right)} {\displaystyle \left(-16{\frac {1}{2}},\infty \right)}
Reversing the Sign
Approach the inequality as you would an equation. Use addition, subtraction, multiplication, and division to move the variable to one side and isolate it. Once you have isolated the variable, you have solved the inequality.
Reverse the inequality sign whenever you multiply or divide by a negative number. When using algebra to solve the inequality, pay close attention whenever you multiply or divide. When you multiply or divide the inequality by a negative number, you must reverse the direction of the inequality sign. For example, to solve the inequality − 5 x > 20 {\displaystyle -5x>20} -5x>20, you need to divide each side by − 5 {\displaystyle -5} -5 to isolate the variable. Thus, you need to reverse the direction of the inequality sign: − 5 x > 20 {\displaystyle -5x>20} -5x>20 − 5 x − 5 > 20 − 5 {\displaystyle {\frac {-5x}{-5}}>{\frac {20}{-5}}} {\frac {-5x}{-5}}>{\frac {20}{-5}} x < − 4 {\displaystyle x<-4} xIn the interval notation : ( − ∞ , − 4 ) {\displaystyle \left(-\infty ,-4\right)} {\displaystyle \left(-\infty ,-4\right)}
Reverse the inequality sign whenever you take the reciprocal of both sides. This is only the case if both sides are negative, or if both sides are positive. The reciprocal of a number x {\displaystyle x} x is shown by 1 x {\displaystyle {\frac {1}{x}}} {\frac {1}{x}}. For example, to solve the inequality 6 < 1 x {\displaystyle 6<{\frac {1}{x}}} 6, you would isolate the x {\displaystyle x} x by taking the reciprocal of both sides. Since both sides are positive, you need to reverse the inequality sign: 6 < 1 x {\displaystyle 6<{\frac {1}{x}}} 6 1 6 > x {\displaystyle {\frac {1}{6}}>x} {\displaystyle {\frac {1}{6}}>x}In the interval notation : ( − ∞ , 1 6 ) {\displaystyle \left(-\infty ,{\frac {1}{6}}\right)} {\displaystyle \left(-\infty ,{\frac {1}{6}}\right)}
Solving Sample Problems
Solve this inequality: 3 x + 2 < − 3 x + 6 + 5 x {\displaystyle 3x+2<-3x+6+5x} 3x+2 Combine like terms on the right side of the inequality: 3 x + 2 < 6 + 2 x {\displaystyle 3x+2<6+2x} 3x+2 Move the variable to one side by subtracting 2 x {\displaystyle 2x} 2x from both sides: 3 x + 2 − 2 x < 6 + 2 x − 2 x {\displaystyle 3x+2-2x<6+2x-2x} 3x+2-2x x + 2 < 6 {\displaystyle x+2<6} x+2 Isolate the variable by subtracting 2 from both sides: x + 2 − 2 < 6 − 2 {\displaystyle x+2-2<6-2} x+2-2 x < 4 {\displaystyle x<4} xIn the interval notation : ( − ∞ , 4 ) {\displaystyle \left(-\infty ,4\right)} {\displaystyle \left(-\infty ,4\right)}
Solve this inequality in which you need to reverse the sign: − 6 x − 18 > 12 {\displaystyle -6x-18>12} -6x-18>12 Isolate the variable by adding 18 to both sides: − 6 x − 18 + 18 > 12 + 18 {\displaystyle -6x-18+18>12+18} -6x-18+18>12+18 − 6 x > 30 {\displaystyle -6x>30} -6x>30 Divide both sides by -6. Since you are dividing by a negative number, you need to reverse the inequality sign: − 6 x > 30 {\displaystyle -6x>30} -6x>30 − 6 x − 6 > 30 − 6 {\displaystyle {\frac {-6x}{-6}}>{\frac {30}{-6}}} {\frac {-6x}{-6}}>{\frac {30}{-6}} x < − 5 {\displaystyle x<-5} xIn the interval notation : ( − ∞ , − 5 ) {\displaystyle \left(-\infty ,-5\right)} {\displaystyle \left(-\infty ,-5\right)}
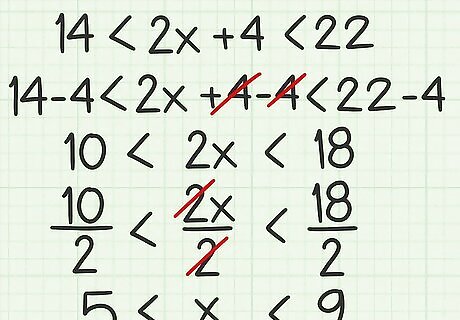
Solve this compound inequality:
14
<
2
x
+
4
<
22
{\displaystyle 14<2x+4<22}
14. An inequality with more than two parts is called a compound inequality. You can solve these the same way you would simple inequalities.
To isolate the variable, subtract 4 from all three parts:
14
−
4
<
2
x
+
4
−
4
<
22
−
4
{\displaystyle 14-4<2x+4-4<22-4}
14-4
10
<
2
x
<
18
{\displaystyle 10<2x<18}
10
Divide each part by 2:
10
2
<
2
x
2
<
18
2
{\displaystyle {\frac {10}{2}}<{\frac {2x}{2}}<{\frac {18}{2}}}
{\frac {10}{2}}
5
<
x
<
9
{\displaystyle 5



















Comments
0 comment