How to Make a Modular Origami Stellated Icosahedron

Making the units

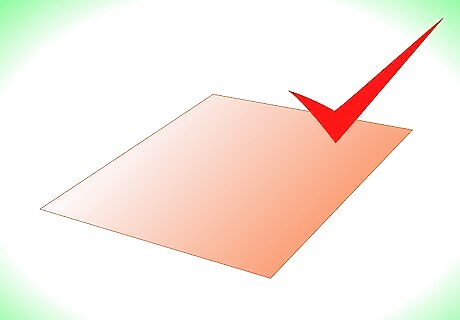
Start with a single sheet of square paper, with each side measuring approximately 3 inches (about 7.5 cm).

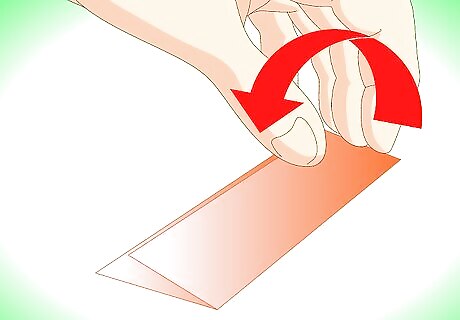
Fold it in half, and make a crease along the fold. If you use origami-paper, make sure the pattern-side is outside and will be visible later.

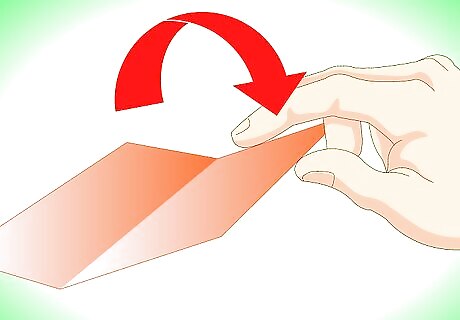
Unfold the previous fold.

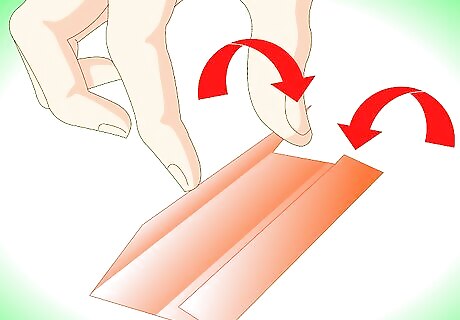
Fold in the right and left sides of the square to meet the crease you just made, to make a rectangle. This is often called a cupboard fold, or book fold.

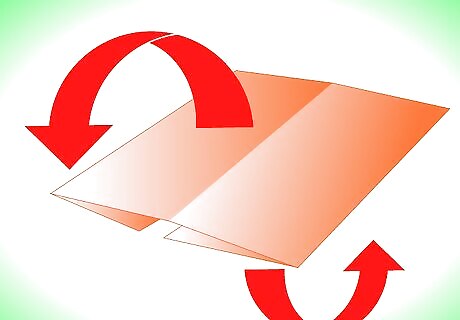
Flip your rectangle over.

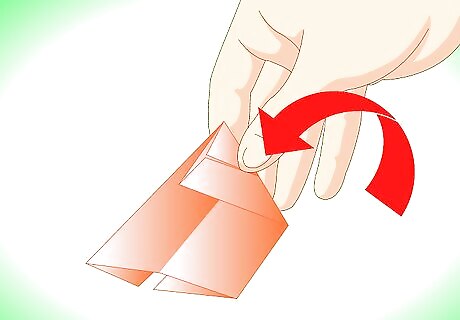
Make a diagonal fold where the top right corner meets the left side of your rectangle. Make sure to fold over both 'doors' of the cupboard fold.

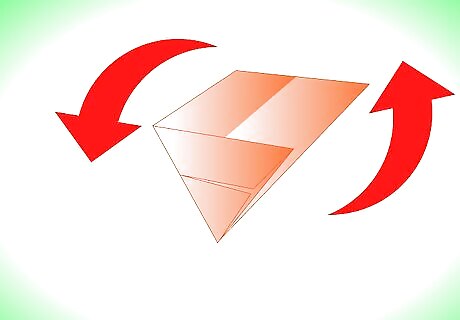
Turn your paper upside down.

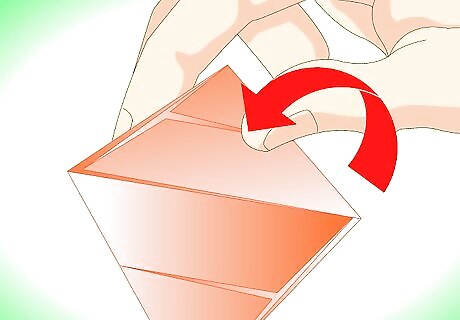
Make another diagonal fold where the top right corner meets the side of this shape. Remember to fold over both 'doors' of the cupboard fold. This makes a parallelogram.

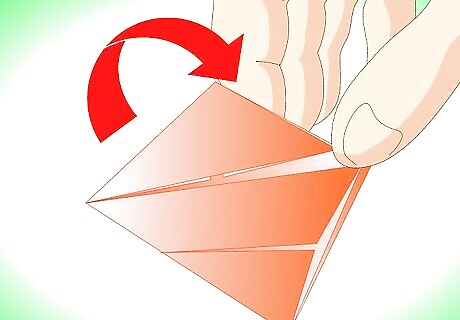
Make a diagonal fold where the top corner meets the right corner of the parallelogram.

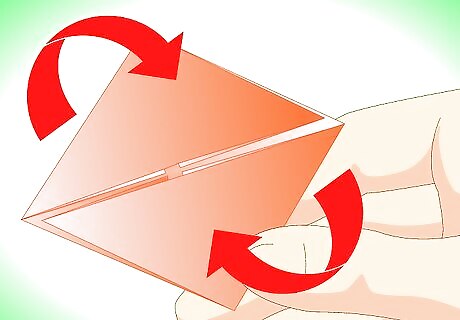
Make another diagonal fold where the bottom corner meets the left corner of the parallelogram. You will end up with a small square.

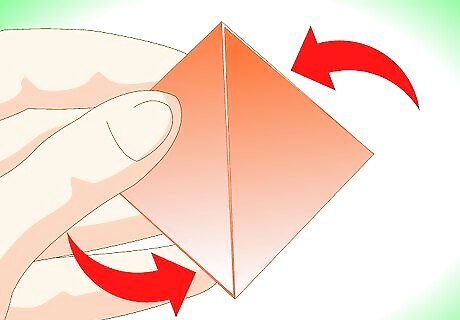
Flip this square over.

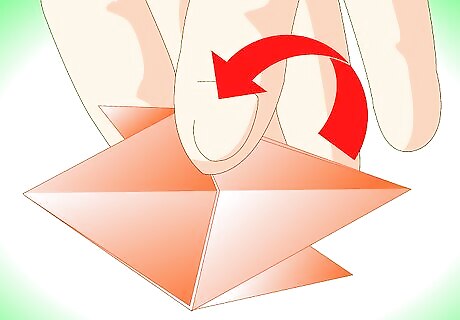
Fold the square in half, making a crease that goes perpendicular to the cupboard fold visible on the square.

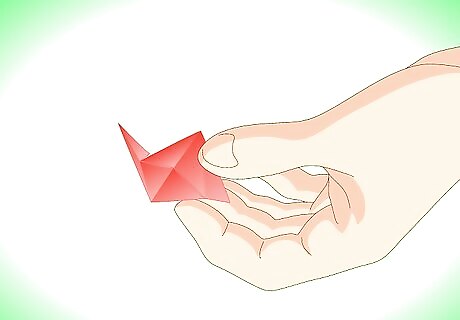
Congratulations! You've made your first unit!

Putting the units together

Make thirty units. If you have three different colors of paper, make ten of each color.

Start putting the units together. The surface of the stellated icosahedron is made up of a number of pyramids (in fact, if you take the regular icosahedron - a solid with twenty triangular faces - and make each face the base of a triangular pyramid, you get a stellated icosahedron). So we start by using the units to make a series of connected pyramids. To get a more simple idea of this complex cube you are now going to build, just think of an only 12-faced regular pentagonal dodecahedron (a Platonic solid), and imagine each of its 20 vertices (5 at the top, 5 at the bottom and 10 around in-between) will be replaced by a pyramid. With 30 units you will shape together those 20 pyramids.

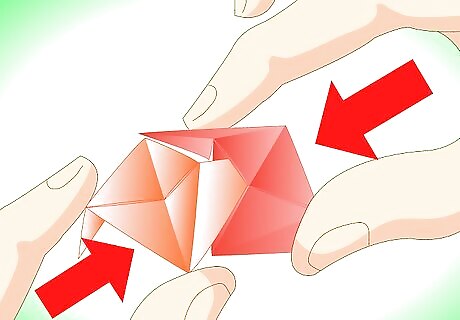
Start with two units of different colors. The triangular ends of each unit are called 'tabs', and the square in the center of the unit contains 'pockets' made up by the cupboard fold that goes along the diagonal. Begin by putting the tab of one unit (pictured in orange below) into the pocket of another (pictured in yellow).

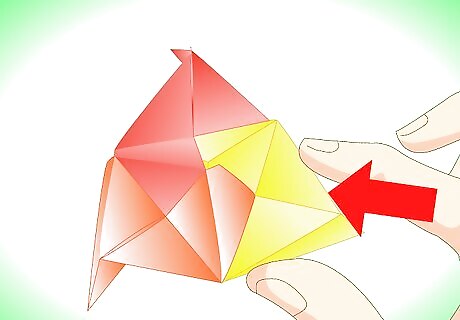
Pick a unit of a different color (pictured red) next and put its tab in the 'orange' pocket, while also inserting the 'yellow' tab in the 'red' pocket. Congratulations - you made your first pyramid!

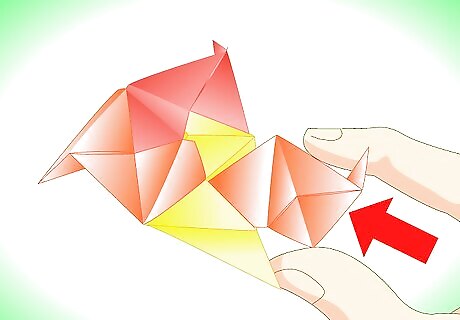
Notice that each unit has two pockets. Continue by taking a new unit (orange in this case), and put its tab in the yellow unit's second pocket.

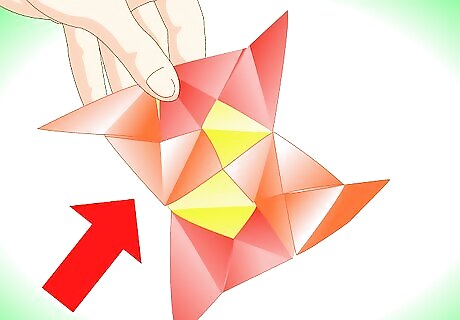
Take a new (red) unit as before, and put its tab in the second orange unit's pocket, also putting the yellow tab in the red unit's pocket. Tada! You now have two adjacent pyramids.

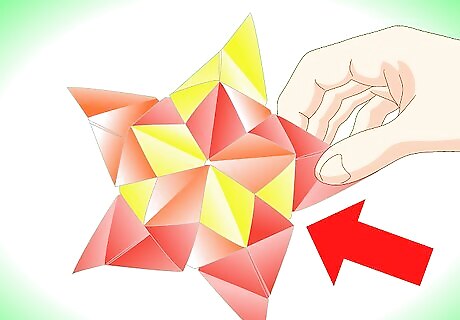
Continue adding pyramids in this manner until you have five pyramids that all meet at a point. If you are using three unit colors, make sure to never put the tab of a unit into a pocket of another unit of the same color. This ensures a regular, colorful pattern on your stellated icosahedron.

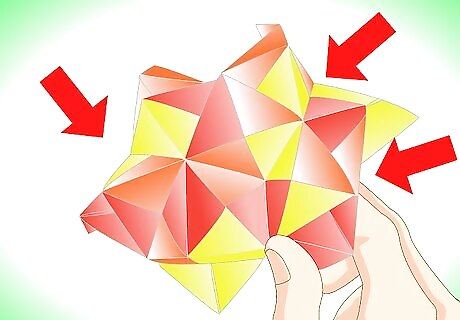
Keep adding pyramids to your stellated icosahedron, making sure that there are never more than five pyramids meeting at a point. You may need to feel your way around a bit to make sure that you never end up having to put a tab into a pocket of the same color. Don't worry if you do - you can carefully prise your units apart and rearrange them until you find a proper arrangement.

Proceed, making sure that no more than five pyramids meet at a point, and your model will take shape. The last unit is tricky - you'll have to make sure that both its tabs go into pockets, and both its pockets are filled by the two remaining free tabs. Proceed with care.

Hooray! You now have a fully formed, colorful, stellated icosahedron.