How to Graph Polar Equations

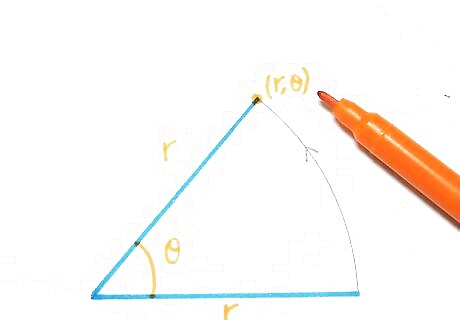
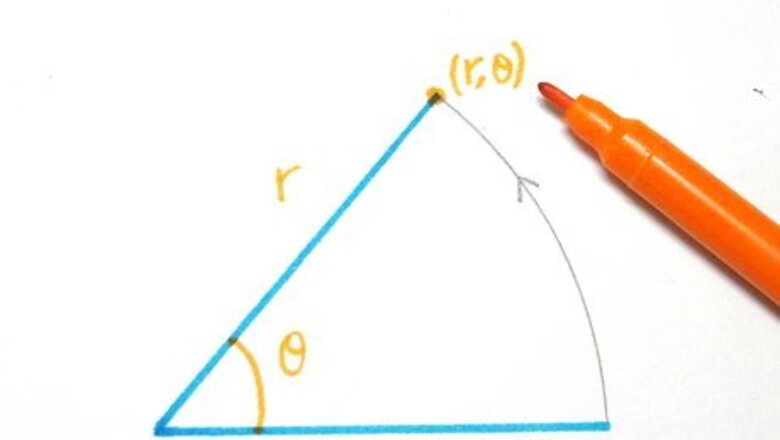
Understand how polar equations work. Coordinates in polar equations are of the form (r,θ), where r represents radius and θ represents angle. This means you rotate θ radians around and go out r units.

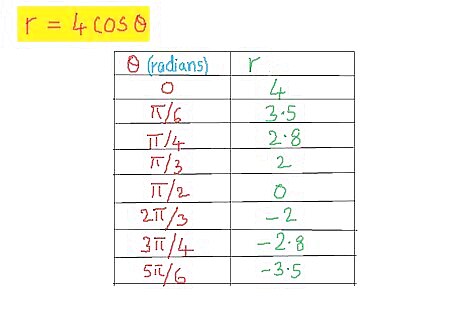
Make a table with values of the angle and radius. Take any random values of θ (around ten values would suffice) and calculate r against each of them using the relationship given between r and θ. This will help you plot them out on a graph easier, because you can just refer to a table instead of having to come up with coordinates in your head.

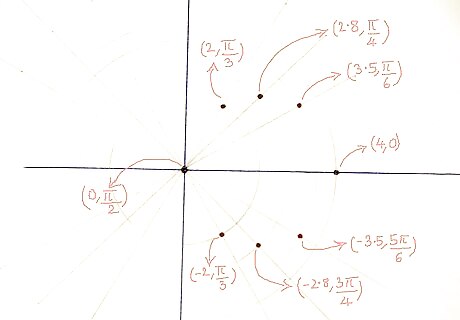
Plot the various (r,θ) points as found in the table. The wikiHow How to Plot Polar Coordinates will be helpful.

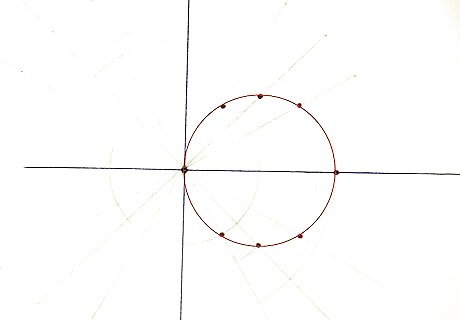
Join the plotted points with a smooth curve and you're done! EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Develop strong graphing skills. Drawing graphs by hand will help you develop foundational graphing skills, especially in understanding scales and axes. This will build a strong base for you to use helpful online tools to visualize complex relationships, perform calculations, and prepare for standardized tests.