How to Find the Area of a Square Using the Length of its Diagonal

Finding the Area from the Diagonal

Draw your square. A square has four equal sides. Let's say each one has a length of "s".

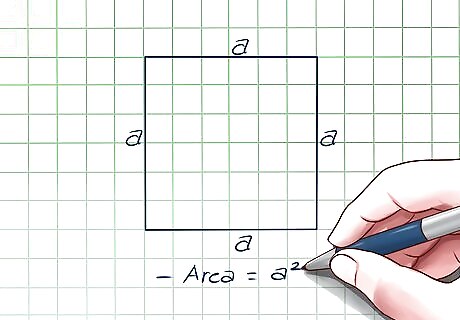
Review the basic formula for a square's area. A square's area is equal to its length times its width. Since each side is s, the formula is Area = s x s = s. This will be useful later on.

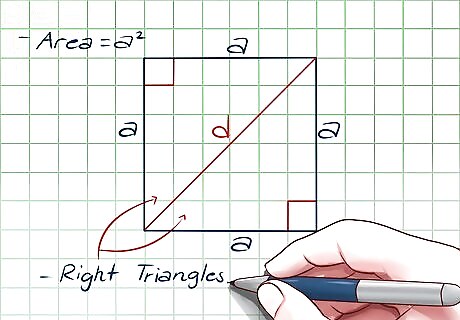
Join any two opposite corners to make a diagonal. Let the measure of this diagonal be d units. This diagonal divides the square into two right-triangles.

Apply the Pythagorean Theorem to one of the triangles. The Pythagorean theorem is a formula for finding the hypotenuse (longest side) of a right triangle: (side one) + (side two) = (hypotenuse), or a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{2}+b^{2}=c^{2}. Now that the square is divided in half, you can use this formula on one of the right triangles: The two shorter sides of the triangle are the sides of the square: each one has a length of s. The hypotenuse is the diagonal of the square, d. s 2 + s 2 = d 2 {\displaystyle s^{2}+s^{2}=d^{2}} s^{2}+s^{2}=d^{2} EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Use this visual trick to understand the Pythagorean Theorem. Imagine a right triangle with squares constructed on each leg and the hypotenuse. by rearranging the smaller squares within the larger square, the areas of the smaller squares (a² and b²) will add up visually to the area of the larger square (c²).

Arrange the equation so s is on one side. Remember that we already know the square's area is equal to s. If you can get s alone on side, you'll have a new equation for area: s 2 + s 2 = d 2 {\displaystyle s^{2}+s^{2}=d^{2}} s^{2}+s^{2}=d^{2} Simplify: 2 s 2 = d 2 {\displaystyle 2s^{2}=d^{2}} 2s^{2}=d^{2} Divide both sides by two: s 2 = d 2 2 {\displaystyle s^{2}={\frac {d^{2}}{2}}} s^{2}={\frac {d^{2}}{2}} Area = s 2 = d 2 2 {\displaystyle s^{2}={\frac {d^{2}}{2}}} s^{2}={\frac {d^{2}}{2}} Area = d 2 2 {\displaystyle {\frac {d^{2}}{2}}} {\frac {d^{2}}{2}}

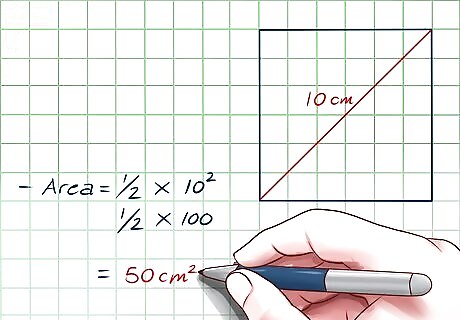
Use this formula on an example square. These steps have proven that the formula Area = d 2 2 {\displaystyle {\frac {d^{2}}{2}}} {\frac {d^{2}}{2}} works for all squares. Just plug in the length of the diagonal for d and solve. For example, let's say a square has a diagonal that measures 10 cm. Area = 10 2 2 {\displaystyle {\frac {10^{2}}{2}}} {\frac {10^{2}}{2}}= 100 2 {\displaystyle {\frac {100}{2}}} {\frac {100}{2}}= 50 square centimeters.

Additional Info

Find the diagonal from the length of a side. The Pythagorean theorem for a square with side s and diagonal d gives you the formula 2 s 2 = d 2 {\displaystyle 2s^{2}=d^{2}} 2s^{2}=d^{2}. Solve for d if you know the side lengths and want to find the length of the diagonal: 2 s 2 = d 2 {\displaystyle 2s^{2}=d^{2}} 2s^{2}=d^{2} 2 s 2 = d 2 {\displaystyle {\sqrt {2s^{2}}}={\sqrt {d^{2}}}} {\sqrt {2s^{2}}}={\sqrt {d^{2}}} s 2 = d {\displaystyle s{\sqrt {2}}=d} s{\sqrt {2}}=d For example, if a square has sides of 7 inches, its diagonal d = 7√2 inches, or about 9.9 inches. If you don't have a calculator, you can use 1.4 as an estimate for √2.

Find the side length from the diagonal. If you are given the diagonal and you know that the diagonal of a square is s 2 {\displaystyle s{\sqrt {2}}} s{\sqrt {2}}, you can divide both sides by 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}} to get s = d 2 {\displaystyle s={\frac {d}{\sqrt {2}}}} s={\frac {d}{{\sqrt {2}}}}. For example, a square with a diagonal of 10cm has sides with length 10 2 = 7.071 {\displaystyle {\frac {10}{\sqrt {2}}}=7.071} {\frac {10}{{\sqrt {2}}}}=7.071 cm. If you need to find both the side length and the area from the diagonal, you can use this formula first, then quickly square the answer to get the area: Area = s 2 = 7.071 2 = 50 {\displaystyle =s^{2}=7.071^{2}=50} =s^{2}=7.071^{2}=50 square centimeters. This is a bit less accurate, since 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}} is an irrational number that can lead to rounding errors.

Interpret the area formula. The math checks out for the formula Area = d 2 2 {\displaystyle {\frac {d^{2}}{2}}} {\frac {d^{2}}{2}}, but is there a way to test this directly? Well, d 2 {\displaystyle d^{2}} d^{2} is the area of a second square with the diagonal as a side. Since the full formula is d 2 2 {\displaystyle {\frac {d^{2}}{2}}} {\frac {d^{2}}{2}}, you can reason that this second square has exactly twice the area of the original square. You can test this yourself: Draw a square on a piece of paper. Make sure all the sides are equal. Measure the diagonal. Draw a second square using that measurement as the length of the square. Trace a copy of your first square so you have two of them. Cut all three squares out. Cut apart the two smaller squares into any shapes so you can arrange them to fit inside the large square. They should fill the space perfectly, showing that the area of the larger square is exactly twice the area of the smaller square.