How to Find Scale Factor

Finding the Scale Factor of Similar Figures

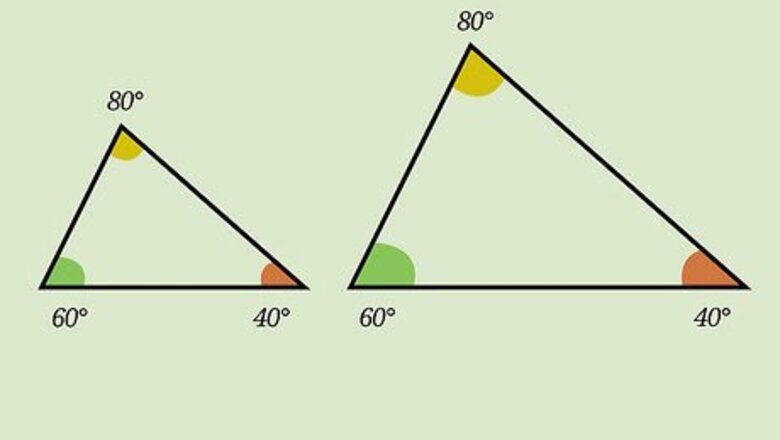
Verify that the figures are similar. Similar figures, or shapes, are ones in which the angles are congruent, and the side lengths are in proportion. Similar figures are the same shape, only one figure is bigger than the other. The problem should tell you that the shapes are similar, or it might show you that the angles are the same, and otherwise indicate that the side lengths are proportional, to scale, or that they correspond to each other.

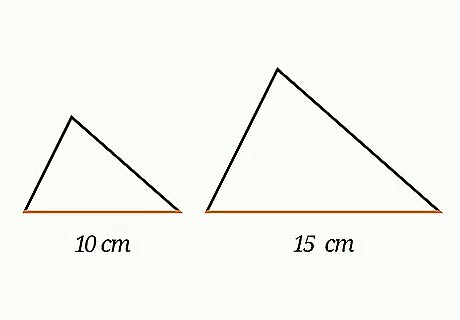
Find a corresponding side length on each figure. You may need to rotate or flip the figure so that the two shapes align and you can identify the corresponding side lengths. You should be given the length of these two sides, or should be able to measure them. If you do not know at least one side length of each figure, you cannot find the scale factor. For example, you might have a triangle with a base that is 15 cm long, and a similar triangle with a base that is 10 cm long.

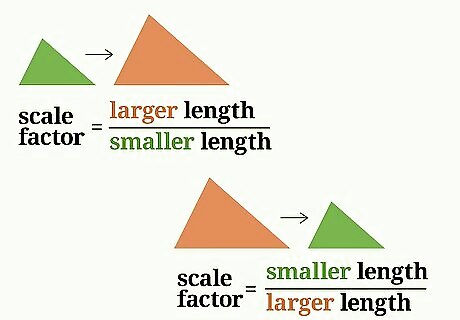
Set up a ratio. For each pair of similar figures, there are two scale factors: one you use when scaling up, and one you use when scaling down. If you are scaling up from a smaller figure to a larger one, use the ratio Scale Factor = l a r g e r l e n g t h s m a l l e r l e n g t h {\displaystyle {\text{Scale Factor}}={\frac {largerlength}{smallerlength}}} {\text{Scale Factor}}={\frac {largerlength}{smallerlength}}. If you are scaling down from a larger figure to a smaller one, use the ratio Scale Factor = s m a l l e r l e n g t h l a r g e r l e n g t h {\displaystyle {\text{Scale Factor}}={\frac {smallerlength}{largerlength}}} {\text{Scale Factor}}={\frac {smallerlength}{largerlength}}. For example if you are scaling down from a triangle with a 15 cm base to one with a 10 cm base, you would use the ratio Scale Factor = s m a l l e r l e n g t h l a r g e r l e n g t h {\displaystyle {\text{Scale Factor}}={\frac {smallerlength}{largerlength}}} {\text{Scale Factor}}={\frac {smallerlength}{largerlength}}.Filling in the appropriate values, it becomes Scale Factor = 10 15 {\displaystyle {\text{Scale Factor}}={\frac {10}{15}}} {\text{Scale Factor}}={\frac {10}{15}}.

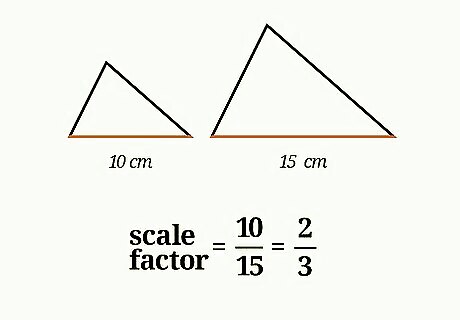
Simplify the ratio. The simplified ratio, or fraction, will give you your scale factor. If you are scaling down, your scale factor will be a proper fraction. If you are scaling up, it will be a whole number or improper fraction, which you can convert to a decimal. For example, the ratio 10 15 {\displaystyle {\frac {10}{15}}} {\frac {10}{15}} simplifies to 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}}. So the scale factor of two triangles, one with a base of 15 cm and one with a base of 10 cm, is 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}}.

Finding a Similar Figure Using the Scale Factor

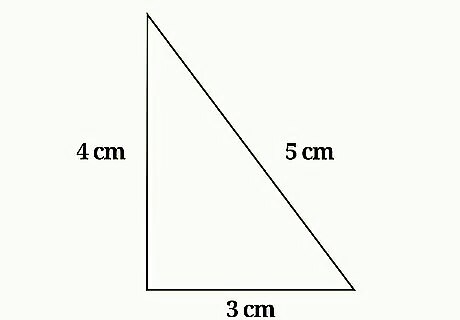
Find the side lengths of the figure. You should have one figure of which the side lengths are given or measurable. If you cannot determine the side lengths of the figure, you cannot make a similar figure. For example, you might have a right triangle with sides measuring 4 cm and 3 cm, and a hypotenuse 5 cm long.

Determine whether you are scaling up or down. If you are scaling up, your missing figure will be larger, and the scale factor will be a whole number, improper fraction, or decimal. If you are scaling down your missing figure will be smaller, and your scale factor will most likely be a proper fraction. For example, if the scale factor is 2, then you are scaling up, and a similar figure will be larger than the one you have.

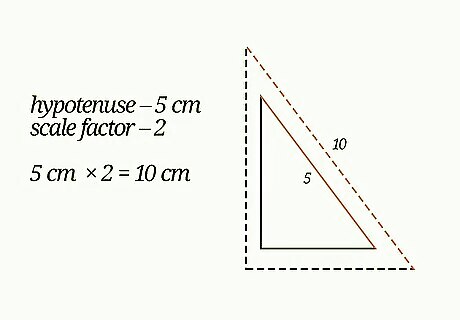
Multiply one side length by the scale factor. The scale factor should be given to you. When you multiply the side length by the scale factor, this gives you the missing corresponding side length on the similar figure. For example, if the hypotenuse of a right triangle is 5 cm long, and the scale factor is 2, to find the hypotenuse of the similar triangle, you would calculate 5 × 2 = 10 {\displaystyle 5\times 2=10} 5\times 2=10. So the similar triangle has a hypotenuse that is 10 cm long.

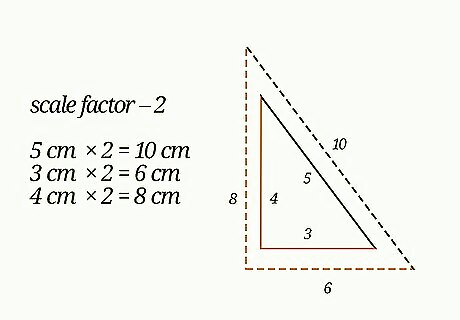
Find the remaining side lengths of the figure. Continue to multiply each side length by the scale factor. This will give you the corresponding side lengths of the missing figure. For example, if the base of a right triangle is 3 cm long, with a scale factor of 2, you would calculate 3 × 2 = 6 {\displaystyle 3\times 2=6} 3\times 2=6 to find the base of the similar triangle. If the height of a right triangle is 4 cm long, with a scale factor of 2 you would calculate 4 × 2 = 8 {\displaystyle 4\times 2=8} 4\times 2=8 to find the height of the similar triangle.

Completing Sample Problems

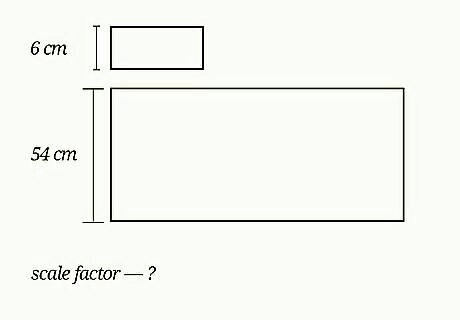
Find the scale factor of these similar figures: a rectangle with a height of 6 cm, and a rectangle with a height of 54 cm. Create a ratio comparing the two heights. Scaling up, the ratio is Scale Factor = 54 6 {\displaystyle {\text{Scale Factor}}={\frac {54}{6}}} {\text{Scale Factor}}={\frac {54}{6}}. Scaling down, the ratio is Scale Factor = 6 54 {\displaystyle {\text{Scale Factor}}={\frac {6}{54}}} {\text{Scale Factor}}={\frac {6}{54}}. Simplify the ratio. The ratio 54 6 {\displaystyle {\frac {54}{6}}} {\frac {54}{6}} simplifies to 9 1 = 9 {\displaystyle {\frac {9}{1}}=9} {\frac {9}{1}}=9. The ratio 6 54 {\displaystyle {\frac {6}{54}}} {\frac {6}{54}} simplifies to 1 9 {\displaystyle {\frac {1}{9}}} {\frac {1}{9}}. So the two rectangles have a scale factor of 9 {\displaystyle 9} 9 or 1 9 {\displaystyle {\frac {1}{9}}} {\frac {1}{9}}.

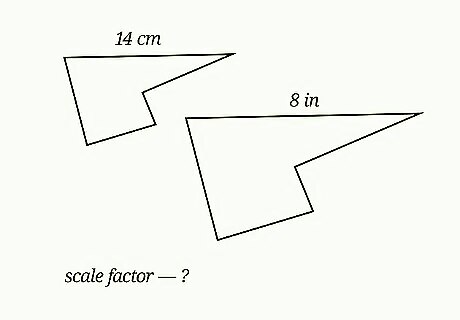
Try this problem. An irregular polygon is 14 cm long at its widest point. A similar irregular polygon is 8 inches at its widest point. What is the scale factor? Irregular figures can be similar if all of their sides are in proportion. Thus, you can calculate a scale factor using any dimension you are given. Since you know the width of each polygon, you can set up a ratio comparing them. Scaling up, the ratio is Scale Factor = 14 8 {\displaystyle {\text{Scale Factor}}={\frac {14}{8}}} {\text{Scale Factor}}={\frac {14}{8}}. Scaling down, the ratio is Scale Factor = 8 14 {\displaystyle {\text{Scale Factor}}={\frac {8}{14}}} {\text{Scale Factor}}={\frac {8}{14}}. Simplify the ratio. The ratio 14 8 {\displaystyle {\frac {14}{8}}} {\frac {14}{8}} simplifies to 7 4 = 1 3 4 = 1.75 {\displaystyle {\frac {7}{4}}=1{\frac {3}{4}}=1.75} {\frac {7}{4}}=1{\frac {3}{4}}=1.75. The ratio 8 14 {\displaystyle {\frac {8}{14}}} {\frac {8}{14}} simplifies to 4 7 {\displaystyle {\frac {4}{7}}} {\frac {4}{7}}. So the two irregular polygons have a scale factor of 1.75 {\displaystyle 1.75} 1.75 or 4 7 {\displaystyle {\frac {4}{7}}} {\frac {4}{7}}.

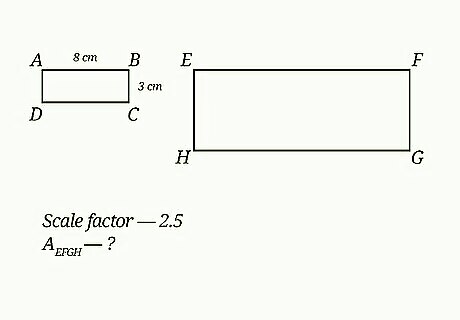
Use the scale factor to answer this problem. Rectangle ABCD is 8cm x 3cm. Rectangle EFGH is a larger, similar rectangle. Using a scale factor of 2.5, what is the area of Rectangle EFGH? Multiply the height of Rectangle ABCD by the scale factor. This will give you the height of Rectangle EFGH: 3 × 2.5 = 7.5 {\displaystyle 3\times 2.5=7.5} 3\times 2.5=7.5. Multiply the width of Rectangle ABCD by the scale factor. This will give you the width of Rectangle EFGH: 8 × 2.5 = 20 {\displaystyle 8\times 2.5=20} 8\times 2.5=20. Multiply the height and width of Rectangle EFGH to find the area: 7.5 × 20 = 150 {\displaystyle 7.5\times 20=150} 7.5\times 20=150. So, the area of Rectangle EFGH is 150 square centimeters.

Finding the Scale Factor in Chemistry

Divide the molar mass of the compound by that of the empirical formula. When you have the empirical formula of a chemical compound and you need to find the molecular formula of that same chemical compound, you can find the scaling factor you need by dividing the molar mass of the compound by the molar mass of the empirical formula. For example, you might need to find the molar mass of an H2O compound with a molar mass of 54.05 g/mol. The molar mass of H2O is 18.0152 g/mol. Find the scaling factor by dividing the molar mass of the compound by the molar mass of the empirical formula: Scaling factor = 54.05 / 18.0152 = 3

Multiply the empirical formula by the scaling factor. Multiply the subscripts of each element within the empirical formula by the scaling factor you just calculated. This will give you the molecular formula of the chemical compound sample involved in the problem. For example, to find the molecular formula of the compound in question, multiply the subscripts of H20 by the scaling factor of 3. H2O * 3 = H6O3

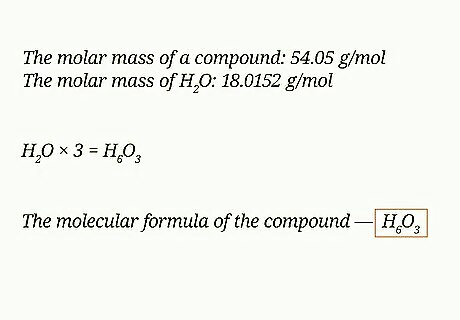
Write the answer. With this answer, you have successfully found the answer to the empirical formula as well as the molecular formula of the chemical compound involved in the problem. For example, the scaling factor for the compound is 3. The molecular formula of the compound is H6O3.