views
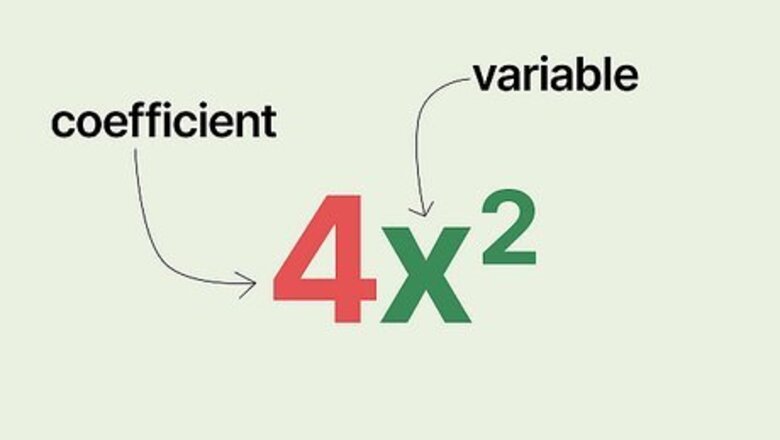
- A term is a coefficient, variable, or both.
- Monomials have 1 term. Binomials have 2 terms. Trinomials have 3 terms.
- Classify by degree by identifying the highest exponent in the polynomial.
Classify by Terms
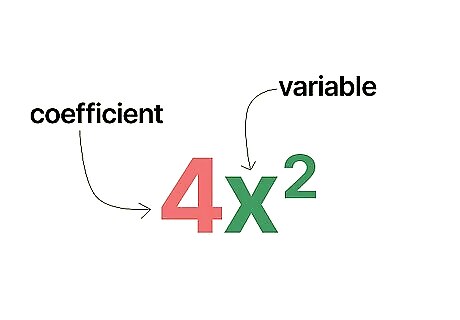
Identify the number of terms. A term consists of a coefficient, variable, or both. For example, you could have 4 {\displaystyle 4} 4, x 2 {\displaystyle x^{2}} x^{2}, or 4 x 2 {\displaystyle 4x^{2}} 4x^{2}. You can use the number of terms to determine the type of polynomial you’re dealing with. Monomials have 1 term. Binomials have 2 terms. Trinomials have 3 terms. Polynomials with more than 3 terms are usually just identified by their degree. The variables should have non-negative integer exponents.
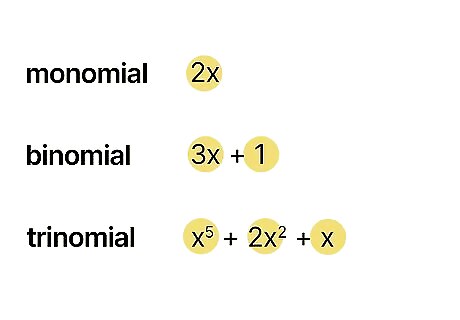
Check out these examples. 2 x {\displaystyle 2x} 2x is a monomial. 7 {\displaystyle 7} 7 is also a monomial, since it can be written as 7 x 0 {\displaystyle 7x^{0}} {\displaystyle 7x^{0}} 3 x + 1 {\displaystyle 3x+1} {\displaystyle 3x+1} is a binomial. x 5 + 2 x 2 + x {\displaystyle x^{5}+2x^{2}+x} {\displaystyle x^{5}+2x^{2}+x} is a trinomial.
Classify by Degree
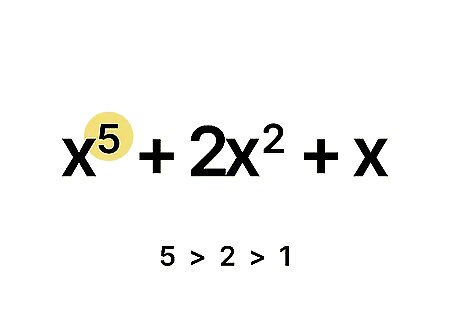
Identify the degree. The degree of a polynomial is the largest exponent present in a term. The standard form is when a polynomial’s terms are arranged in descending order of exponent size. For factoring info, check out our guide on factoring a cubic polynomial.
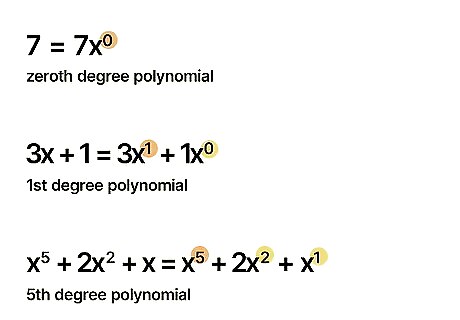
See these examples from the last method: 2 x {\displaystyle 2x} 2x is a 1st degree polynomial. 7 {\displaystyle 7} 7 is a zeroth degree polynomial, since it can be written as 7 x 0 {\displaystyle 7x^{0}} {\displaystyle 7x^{0}}. 3 x + 1 {\displaystyle 3x+1} {\displaystyle 3x+1} is a 1st degree polynomial. x 5 + 2 x 2 + x {\displaystyle x^{5}+2x^{2}+x} {\displaystyle x^{5}+2x^{2}+x} is a 5th degree polynomial.


















Comments
0 comment