views
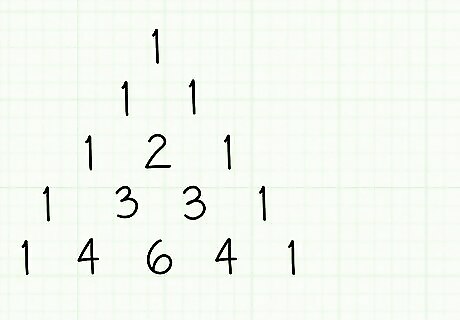
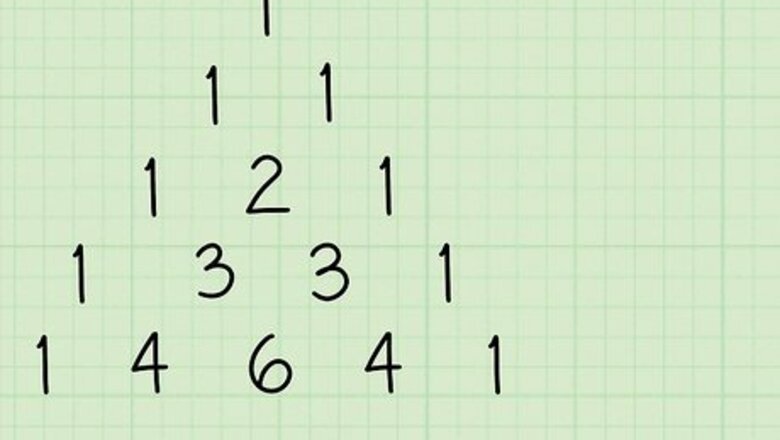
On a blank piece of paper, draw up Pascal's triangle, with some space reserved to the right. Draw the triangle up to at least 5 rows.

On the right of each row of the Pascal's triangle, write (x+y).
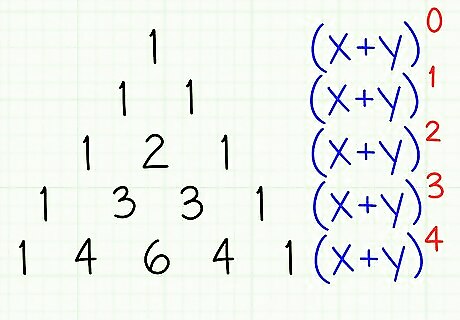
Now, take the power of n, n+1, n+2... onto (x+y). In other terms, start with (x+y), then (x+y), (x+y). Note down the powers. N to the power of 0 is always 1. That means (x+y) is 1. Also, (x+y) is simply (x+y).
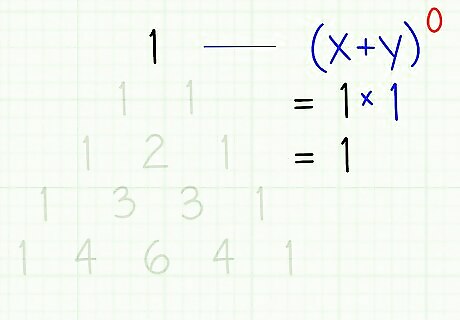
If you can see from Pascal's triangle, the first 1 represents (x+y), with 1 as 0.
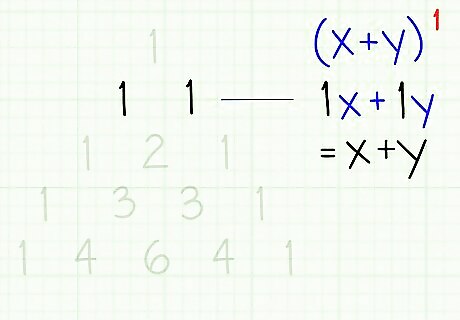
The next row of the Pascal's triangle, (1, 1) represents (x+y), with the first 1 as the coefficient of x, and the second as coefficient of y.
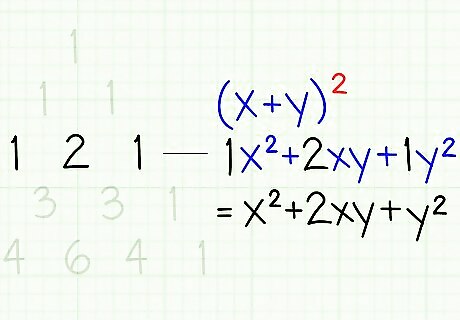
The next row of Pascal's triangle, (1, 2, 1) represents (x+y), with the first 1 as the coefficient of x, second as the coefficient of 2xy and third as coefficient of y.
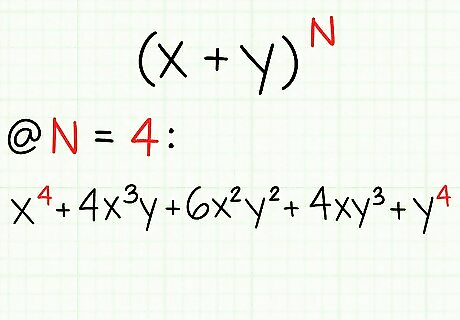
Confused? In mathematical terms, for each 1 you see, except the first line, it will represent either the coefficients of x or y. It will always have the highest power used in your (x+y), which is N. The numbers in a line in Pascal's triangle will refer to the coefficients of each term, with the amount of number in a line referring to the total amount of terms related to (x+y).
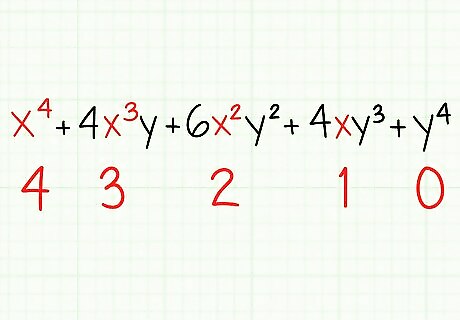
Each x term power will decrease over the terms, like: x, then x, then x, and then 1: which represents NIL in this process.
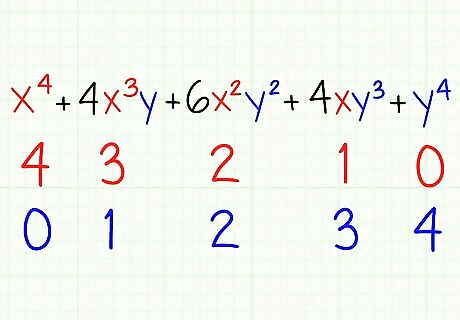
Each y term power will increase over the terms, like: , 1: which represents NIL in this process, y, then y, then y. Example: (x+y) Since the power (n) = 4, we should have a look at the fifth (n+1) row of the Pascal triangle. Thus, the (n + 1 = 5) row of the Pascal triangle is:1 4 6 4 1 Therefore, 1 4 6 4 1 represent the coefficients of the terms of x & y after expansion of (x+y). The answer: x+4xy+6xy+4xy+y




















Comments
0 comment