views
Adding Fractions
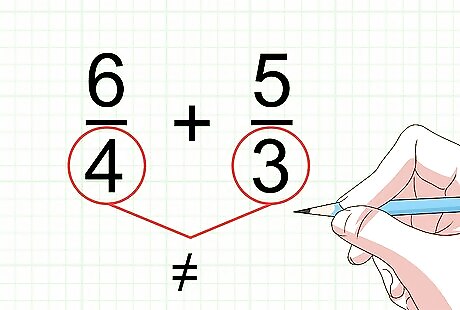
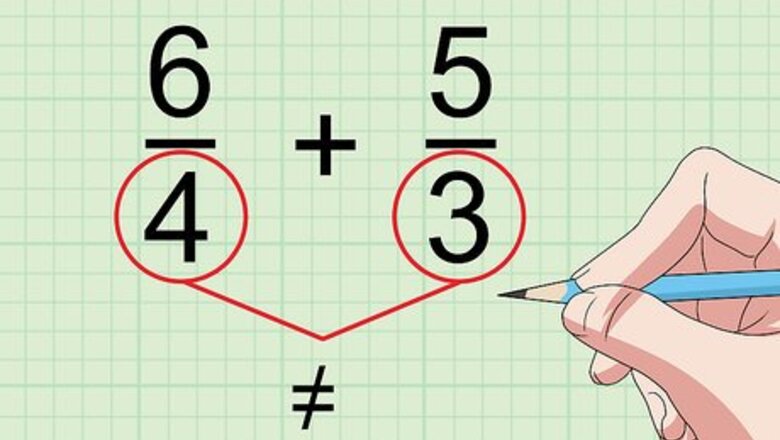
Look at the denominators. The denominator is the number below the fraction bar. In order to add fractions, the denominators of the fractions have to be the same. If they are not the same, you will need to find the lowest common denominator. The denominator tells you how many pieces make one whole. If the two fractions do not use the same denominator, then you are not adding same-sized pieces, and your answer will be incorrect. For example, if you are adding the fractions 6 4 {\displaystyle {\frac {6}{4}}} {\frac {6}{4}} and 5 3 {\displaystyle {\frac {5}{3}}} {\frac {5}{3}}, you would compare the 4 and the 3. They are different, and so you cannot add these fractions as is, because you cannot add fourths and thirds together.
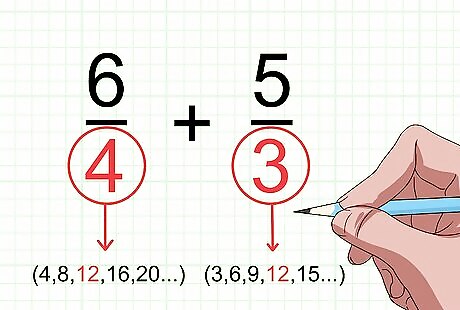
Find the lowest common denominator (LCD) of the two fractions. If the denominators are the same, you can skip this step. If the denominators are not the same, you must find the LCD. To find the LCD, you are looking for the lowest common multiple of the two denominators. A multiple is a number that results from multiplying a number by another number. One way to find the LCD is to make a list of multiples of the two denominators until you find one that matches. To learn other ways to find the LCD, read Find the Least Common Denominator. For example, if your denominators are 4 and 3, first list multiples of 4 (4, 8, 12, 16, 20...) and then list multiples of 3 (3, 6, 9, 12, 15…). The lowest multiple the two numbers have in common is 12, so 12 is the least common denominator.
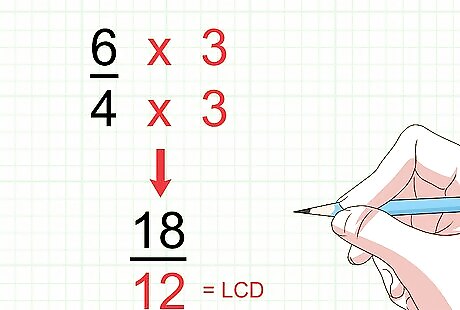
Find the new numerator of the first fraction. The numerator is the number above the fraction bar. To find the new numerator, compare the original denominator to the LCD. Determine what factor you have to multiply the original denominator by to get to the LCD. Then, multiply the numerator by this same factor. The numerator tells you how many pieces you have. Just remember when preparing fractions for adding that whatever you do to the denominator, you must also do to the numerator. For example, if the original denominator was 4, and the LCD is 12, you would have to multiply the original denominator by the factor 3, since 4 × 3 = 12 {\displaystyle 4\times 3=12} 4\times 3=12. As such, you would then multiply the numerator by the factor 3. If the original numerator was 6, then the new numerator would be 18, since 6 × 3 = 18 {\displaystyle 6\times 3=18} 6\times 3=18. So, your new fraction becomes 18 12 {\displaystyle {\frac {18}{12}}} {\frac {18}{12}}.
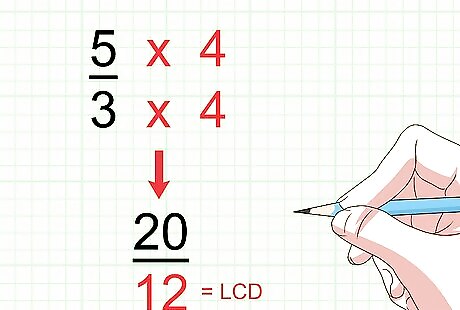
Find the new numerator of the second fraction. To do this, follow the same process you did to find the new numerator for the first fraction. For example, if the original denominator was 3, and the LCD is 12, you would have to multiply the original denominator by the factor 4, since 3 × 4 = 12 {\displaystyle 3\times 4=12} 3\times 4=12. As such, you would then multiply the numerator by the factor 4. If the original numerator was 5, then the new numerator would be 20, since 5 × 4 = 20 {\displaystyle 5\times 4=20} 5\times 4=20. So, your new fraction becomes 20 12 {\displaystyle {\frac {20}{12}}} {\frac {20}{12}}.
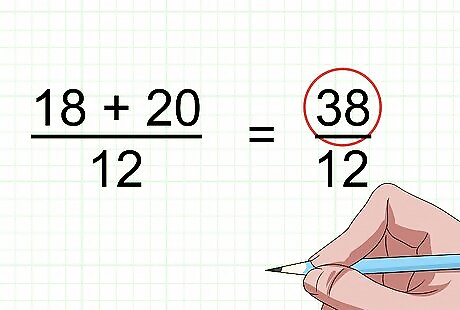
Add the numerators of the two fractions, and place the sum over the LCD. Now that you have found the lowest common denominator, you are adding individual pieces that are the same size, so you can proceed with adding the numerators. You do NOT add the denominators, because the size of the pieces you are adding does not change, only how many of the pieces you have. For example, if you are adding 18 12 + 20 12 {\displaystyle {\frac {18}{12}}+{\frac {20}{12}}} {\frac {18}{12}}+{\frac {20}{12}}, you will add the numerators 18 and 20. 18 + 20 = 38 {\displaystyle 18+20=38} 18+20=38. Then, you will place 38 over the LCD, which is 12. So the sum is 38 12 {\displaystyle {\frac {38}{12}}} {\frac {38}{12}}.
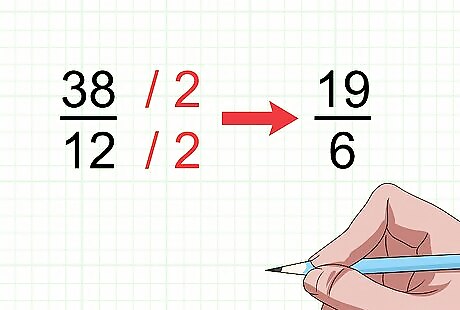
Simplify your answer, if possible. Usually you will be asked to reduce, or simplify a final answer if it is a fraction. To simplify, find the highest number that will divide evenly into the numerator and denominator, then divide the numerator and denominators by that number. For example, if your answer is 38 12 {\displaystyle {\frac {38}{12}}} {\frac {38}{12}}, divide the numerator and denominator by 2. 38 / 2 = 19 {\displaystyle 38/2=19} 38/2=19 and 12 / 2 = 6 {\displaystyle 12/2=6} 12/2=6, so the simplified fraction is 19 6 {\displaystyle {\frac {19}{6}}} {\frac {19}{6}}. Since 19 cannot be divided evenly by any other number, you cannot simplify 19 6 {\displaystyle {\frac {19}{6}}} {\frac {19}{6}}any further. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Simplifying a fraction just changes the way the fraction is written. To simplify a fraction, you can cancel out the greatest common factor from the numerator and denominator or convert an improper fraction to a mixed number. This doesn't change the inherent value of the fraction.
Multiplying Fractions
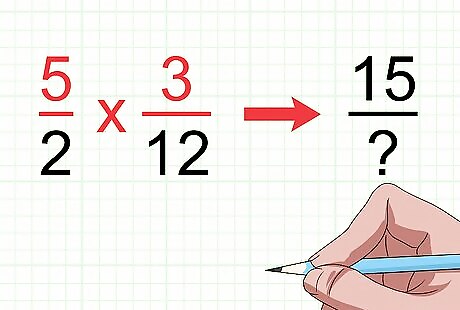
Multiply the numerators. This will give you the numerator of the product. The numerators are the numbers above the fraction bar. The product is the answer to a multiplication problem. Unlike when adding fractions, multiplying fractions does not require having a least common denominator. This is because when taking a part of a fraction, you are changing the number of pieces in the whole. For example, if you are multiplying 5 2 {\displaystyle {\frac {5}{2}}} {\frac {5}{2}} and 3 12 {\displaystyle {\frac {3}{12}}} {\frac {3}{12}}, the numerator of your answer (product) will be 15, since 5 × 3 = 15 {\displaystyle 5\times 3=15} 5\times 3=15.
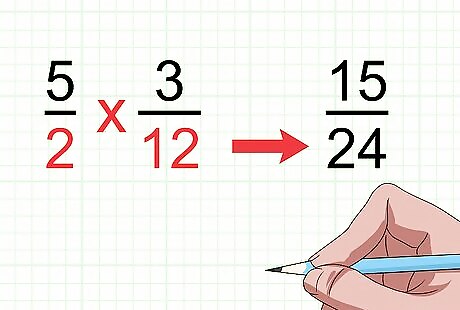
Multiply the denominators. This will give you the denominator of the product. The denominators are the numbers below the fraction bar. For example, if you are multiplying 5 2 {\displaystyle {\frac {5}{2}}} {\frac {5}{2}} and 3 12 {\displaystyle {\frac {3}{12}}} {\frac {3}{12}}, the denominator of your product will be 24, since 2 × 12 = 24 {\displaystyle 2\times 12=24} 2\times 12=24.
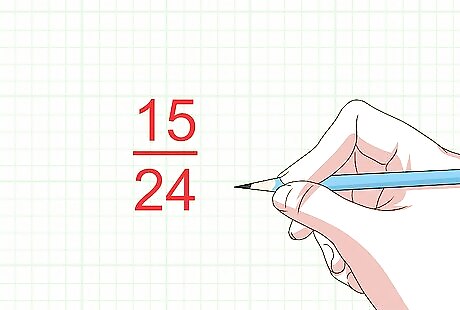
Write your new product. To get the product of the two fractions, simply put together the numerator and denominator you found by multiplying. For example, if you found the numerator by multiplying 5 × 3 {\displaystyle 5\times 3} 5\times 3 and the denominator by multiplying 2 × 12 {\displaystyle 2\times 12} 2\times 12, your answer (product) is 15 24 {\displaystyle {\frac {15}{24}}} {\frac {15}{24}}.
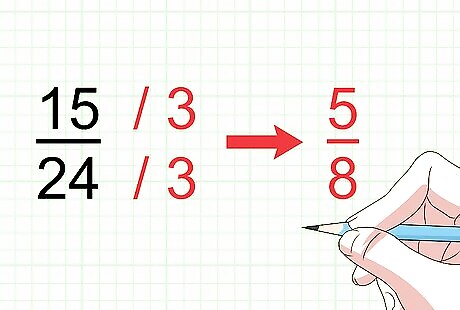
Simplify your answer, if possible. Usually you will be asked to reduce, or simplify a final answer if it is a fraction. To simplify, find the highest number that will divide evenly into the numerator and denominator, then divide the numerator and denominators by that number. For example, if your answer is 15 24 {\displaystyle {\frac {15}{24}}} {\frac {15}{24}}, you can divide the numerator and denominator evenly by 3. 15 / 3 = 5 {\displaystyle 15/3=5} 15/3=5 and 24 / 3 = 8 {\displaystyle 24/3=8} 24/3=8, so the simplified fraction is 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}}. Since 5 cannot be divided evenly by any other number, you cannot simplify 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}} any further.



















Comments
0 comment