The Easiest Way to Round to the Nearest Hundred

• Round down if the tens digit is ${\displaystyle 0,1,2,3,}$ or ${\displaystyle 4}$.
• Round up if the tens digit is ${\displaystyle 5,6,7,8,}$ or ${\displaystyle 9}$.
• Add ${\displaystyle 1}$ to the hundreds digit to round up. Leave the hundreds digit the same when rounding down.
• Change all the digits to the right of the hundreds place to ${\displaystyle 0}$ after rounding.

Finding the Nearest Hundred

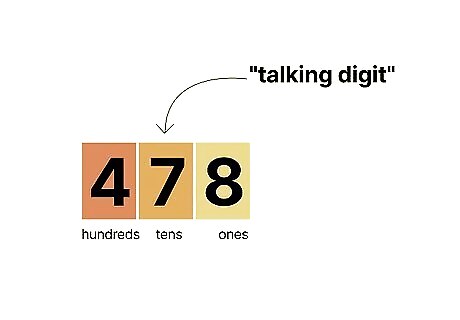
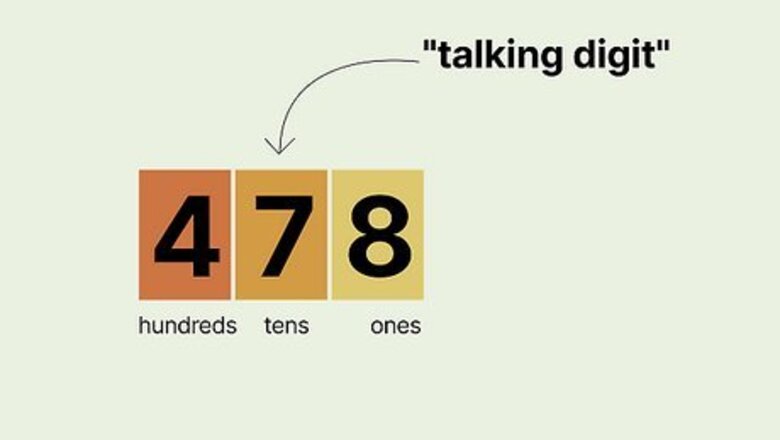
Look at the digit in the tens place. As you probably guessed by "nearest" hundred, rounding is all about distance. The tens digit, the one just to the right of the hundreds digit, tells you which hundreds digit your number is closest to—that's why it's sometimes called the "talking digit." For example, in 478 {\displaystyle 478} {\displaystyle 478}, the "talking digit" in the tens place is a 7 {\displaystyle 7} 7. Using a number line can help you easily visualize which hundred your number is closest to.

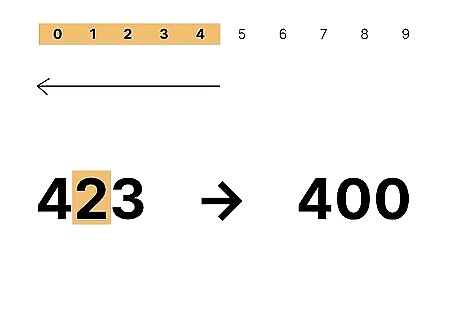
Round down if the tens digit is , 1 , 2 , 3 , {\displaystyle 0,1,2,3,} {\displaystyle 0,1,2,3,} or 4 {\displaystyle 4} 4. When the tens digit is 0 , 1 , 2 , 3 , {\displaystyle 0,1,2,3,} {\displaystyle 0,1,2,3,} or 4 {\displaystyle 4} 4, the number is closer to the lower hundred than it is to the higher hundred. To round these numbers, just drop the extra digits and stay with the original hundreds digit. For example, in 423 {\displaystyle 423} {\displaystyle 423}, the tens digit is the talking digit, and it's a 2 {\displaystyle 2} {\displaystyle 2}. So you'd round down to 400 {\displaystyle 400} {\displaystyle 400}.

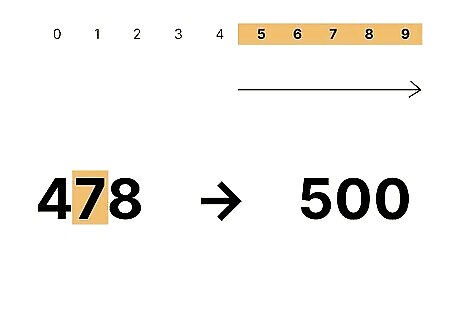
Round up if the tens digit is 5 , 6 , 7 , {\displaystyle 5,6,7,} {\displaystyle 5,6,7,} or 8 {\displaystyle 8} 8. The 5 {\displaystyle 5} 5 is a little weird—technically it's equally close to both hundreds! But it's rounded up just to keep the rule simple. For example, in 478 {\displaystyle 478} {\displaystyle 478}, the tens digit is a 7 {\displaystyle 7} 7, so you'd round up to 500 {\displaystyle 500} {\displaystyle 500}.

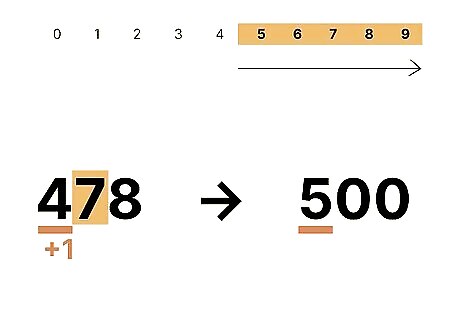
Add 1 {\displaystyle 1} 1 to the hundreds digit if you rounded up. When you round up, you basically give the number credit for another full hundred, even though it's not quite there. It's close enough! So you just add another 1 {\displaystyle 1} 1. For example, as you saw with 478 {\displaystyle 478} {\displaystyle 478}, the 7 {\displaystyle 7} 7 in the tens place means you need to round up, so you'd add 1 {\displaystyle 1} 1 to 400 {\displaystyle 400} {\displaystyle 400} to get 500 {\displaystyle 500} {\displaystyle 500}. If you round down, the hundreds digit stays the same. For example, 423 {\displaystyle 423} {\displaystyle 423} gets rounded down to 400 {\displaystyle 400} {\displaystyle 400} because the digit in the tens place is 2 {\displaystyle 2} {\displaystyle 2}.

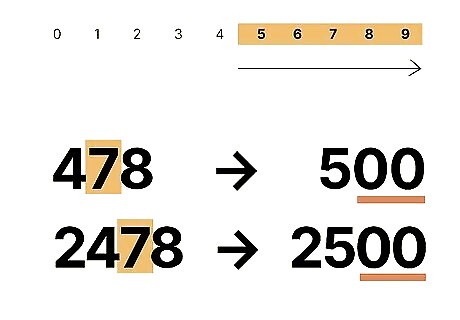
Change all the digits to the right of the hundreds place to {\displaystyle 0} {\displaystyle 0}. The rounding takes care of all the numbers to the right—that's what makes it easier to do math with rounded numbers. Any numbers to the left of the hundreds place, on the other hand, are going to stay the same. For example, if you have 478 {\displaystyle 478} {\displaystyle 478} and you're rounding to the nearest hundred, you get 500 {\displaystyle 500} {\displaystyle 500}. But what if you have 2 , 478 {\displaystyle 2,478} {\displaystyle 2,478}? The numbers to the left stay the same, so if you're rounding it to the nearest hundred, you get 2 , 500 {\displaystyle 2,500} {\displaystyle 2,500}.

Practice Problems

Round 231 {\displaystyle 231} {\displaystyle 231}, 147 {\displaystyle 147} {\displaystyle 147}, and 981 {\displaystyle 981} {\displaystyle 981} to the nearest hundred. Remember to look at the number in the tens place to decide whether to round up or round down. You've got this!

Round 13 , 167 {\displaystyle 13,167} {\displaystyle 13,167} and 98 , 964 {\displaystyle 98,964} {\displaystyle 98,964} to the nearest hundred. Decide whether to round up or down based on the number in the tens place. Remember to change the numbers to the right of the hundreds digit to 0 {\displaystyle 0} {\displaystyle 0}.

Car shopping word problem. Your mom is shopping for a new car and has a budget of $20,000. The car she's looking at has a starting retail price of $18,000. By rounding to the nearest hundred, determine if she can afford to add the following options: Power sunroof: $725 Rear spoiler: $250

Practice Problem Solutions

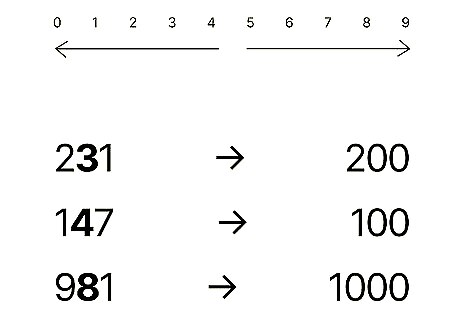
Your rounded numbers are 200 {\displaystyle 200} {\displaystyle 200}, 100 {\displaystyle 100} 100, and 1 , 000 {\displaystyle 1,000} {\displaystyle 1,000}. Did the last one throw you? The number in the tens place is 8 {\displaystyle 8} 8, which means you need to round up. Just add 1 {\displaystyle 1} 1 to the digit in the hundreds place, which is 9 {\displaystyle 9} 9, and you get 10 {\displaystyle 10} 10, so your answer is 1 , 000 {\displaystyle 1,000} {\displaystyle 1,000}. Remember that you're rounding to the nearest hundred. With 147 {\displaystyle 147} {\displaystyle 147}, it would be incorrect to first round the 4 {\displaystyle 4} 4 up to 5 {\displaystyle 5} 5 because of the 7 {\displaystyle 7} 7 in the ones place, and then round up to 200 {\displaystyle 200} {\displaystyle 200}.

Your rounded numbers are 13 , 200 {\displaystyle 13,200} {\displaystyle 13,200} and 99 , 000 {\displaystyle 99,000} {\displaystyle 99,000}. There's another one that carries over to the thousands! But here, you already have a number in the thousands place, 8 {\displaystyle 8} 8. So you'd need to add a 1 {\displaystyle 1} 1 to it to get 99 , 000 {\displaystyle 99,000} {\displaystyle 99,000}.

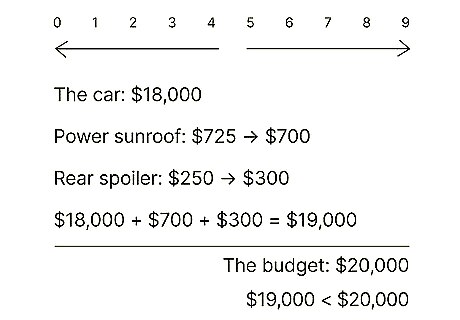
Car shopping word problem. Yes, she can afford the power sunroof and the rear spoiler. Your mom's budget of $20,000 gives her an extra $2,000 over the base price of the car, which is $18,000. You'd find this by subtracting the base price from your mom's budget. Round the cost of each of the two options. The power sunroof is $725, which rounds to $700. The rear spoiler is $250, which rounds to $300. Add your rounded numbers together and you get $1,000. Since you've already established that your mom has an extra $2,000, and $1,000 is less, you can conclude that she can afford the two options she wants.