How to Find the Density of Water

Finding Density of Water

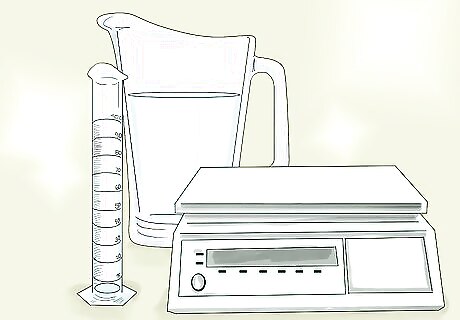
Gather your materials. To calculate the density of water you will need a graduated cylinder, a scale or balance, and water. Graduated cylinders are special containers that have lines or gradations that allow you to measure a specific volume of liquid.

Weigh the empty graduated cylinder. In order to find the density, you have to know the mass and volume of the liquid in question. You will use the graduated cylinder to obtain the mass of the water, but you have to subtract out the weight of the graduated cylinder so you know you’re only measuring the mass of the water itself. Turn the balance on and make sure it is set to zero. Place the dry, empty graduated cylinder on the balance. Record the mass of the cylinder in grams (g). For example, let’s say the empty graduated cylinder weighs 11 grams.

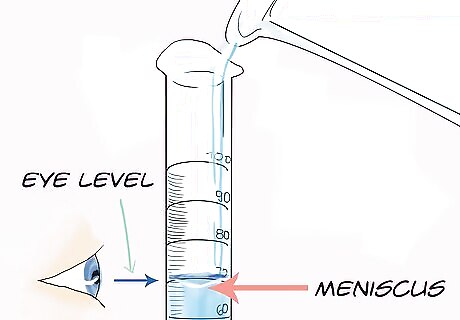
Fill the graduated cylinder with water. It doesn’t matter how much water you add, but be sure to note the exact amount. Read the volume by looking at the cylinder at eye level and recording the volume at the bottom of the meniscus. The meniscus is the curve of the liquid that you’ll see when you look at the water right at eye level. The volume of water in the graduated cylinder is the volume you will use for the density calculation. Let’s say you filled the graduated cylinder with 7.3 milliliters (mL) of volume.

Weigh the water-filled graduated cylinder. Make sure the balance is set to zero and weigh the graduated cylinder full of water. Be careful not to spill any of the water out of the top when you weigh it. If you do spill the water, take note of the new volume and re-weigh the water-filled graduated cylinder. For example, let’s say the full graduated cylinder weighs 18.3 grams.

Subtract the weight of the empty cylinder from the full cylinder. To get the mass of the water only, you must subtract out the weight of the graduated cylinder. The result is the mass of the water in the cylinder. In our example, the mass of the graduated cylinder is 11 g and the mass of the cylinder full of water is 18.3 g. 18.3 g – 11 g = 7.3 g, therefore the mass of the water is 7.3 grams.

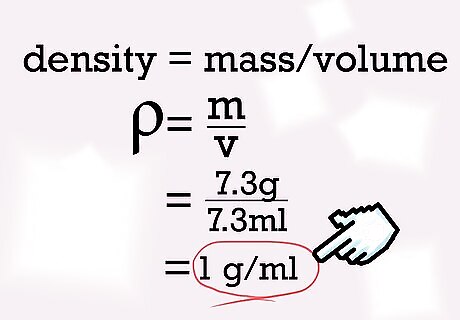
Calculate the density by dividing the mass by the volume. Using the equation density = mass/volume, you can determine the density of water. Plug in the values of mass and volume you determined and solve. Mass of the water: 7.3 g Volume of the water: 7.3 mL Density of water = 7.3/7.3 = 1 g/mL

Understanding Density

Define the equation for density. Density is equal to the mass of an object, m, divided by the volume, v, of that object. Density is represented with the Greek letter rho, ρ. An object that is denser will have a greater mass for a smaller amount of volume compared to an object that is less dense. The standard equation for density is ρ = m/v.

Use the proper units for each variable. When calculating density, it is customary to use metric units. The mass of an object is represented in grams. The volume of the object is in milliliters. You may also see volume in centimeters cubed (cm).

Know why density is important. The density of an object can be used to identify different materials. If you are trying to identify a substance, you can calculate its density and then compare it to the known density of other materials.

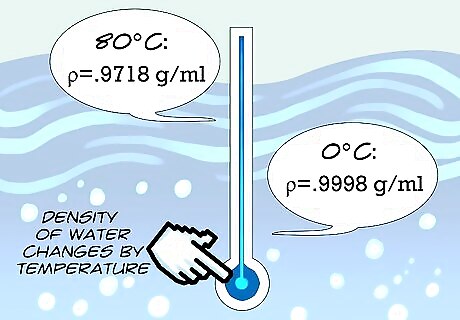
Understand factors that can influence the density of a water. Although the density of water is pretty close to 1 g/mL, certain disciplines of science need to know the density of water with a higher specificity. The density of pure water is altered by temperature. Water density increases as the temperature gets colder. For example, at 0°C the density of water is 0.9998 g/mL, but at 80°C the density is 0.9718 g/mL. These differences may seem small, but are very important to be aware of in scientific experiments and research.