How to Calculate Fractions

Recognizing the Parts of a Fraction

Find a fraction. Fractions are written as 1 number placed over a dividing line with 1 number below it.

Identify the numerator. The number on top is called the numerator and it tells you how many parts of the fraction there are. For example, in the fraction 1/5, 1 is the numerator.

Locate the denominator. The number on the bottom is called the denominator. This number tells you how many parts make up the whole number. For example, in the fraction 1/5, 5 is the denominator so there should be 5 parts in the fraction.

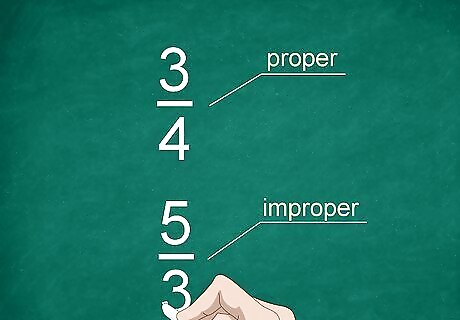
Determine if the fraction is proper or improper. If the numerator is less than the denominator, the fraction is proper. For an improper fraction, the numerator is greater than the denominator. For example, 3/4 is a proper fraction and 5/3 is an improper fraction. If you have a whole number with a fraction, it's called a mixed fraction. For example, 1 1/2 is a mixed fraction.

Adding or Subtracting Fractions

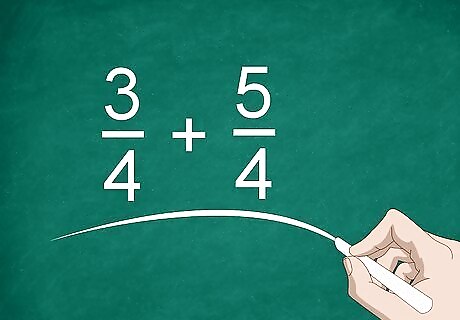
Identify fractions with like denominators. If you need to add or subtract fractions, they need to have common denominators before you make your calculations. Look at the denominator on the fractions to see if they're the same (like).

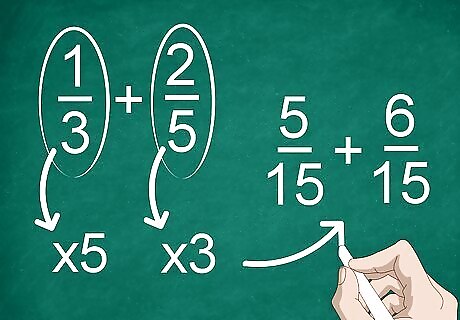
Find a common denominator if the denominators are unlike. If your denominators aren't the same, you'll need to change the fractions so they have the same denominators. To find a common denominator, multiply each part of a fraction by the denominator of the other fraction. For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3. You should get 5/15 + 6/15. Then you can calculate the fractions.

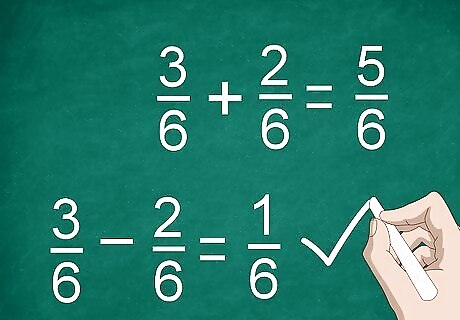
Add or subtract the numerators to calculate the fractions. Once you've found a common denominator and multiplied the numerators if necessary, you're ready to add or subtract. Add or subtract the numerators and place the result over a dividing line. Put the common denominator below the line. For example, 3/6 - 2/6 = 1/6. Avoid adding or subtracting denominators.

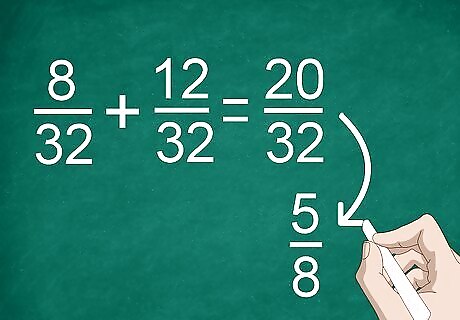
Simply the sum if necessary. If you've had to find a common denominator, you may end up with a large fraction that can be simplified. For example, if you added 8/32 +12/32, you'd get 20/32. This can be reduced to 5/8.

Multiplying and Simplifying Fractions

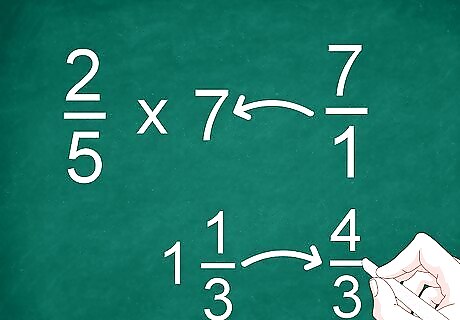
Turn mixed fractions or whole numbers into improper fractions. To make it easier to multiply, you'll need to work with proper or improper fractions. If you have a whole number or mixed fraction that you want to multiply, turn it into its fraction. For example, to multiply 2/5 by 7, turn 7 into a fraction. Then you can multiply 2/5 by 7/1. If you have a mixed fraction such as 1 1/3, turn it into an improper fraction, 4/3 before you multiply.

Multiply the numerators and denominators. Instead of adding the numerators, multiply both of them and write the result over your dividing line. You'll also need to multiply the denominators and put the result under the line. For example, to multiply 1/3 by 3/4, multiply 1 by 3 to get the numerator. Multiply 3 by 4 to get the denominator. Your answer will be 3/12.

Simplify your result. In many cases, you'll need to reduce the result to a simplified fraction, especially if you started with improper fractions. Identify the greatest common factor and use it to simplify the numerator and denominator. For example, if your answer is 3/12, 3 is the greatest common factor. Reduce the fraction by 3 to get 1/4.

Dividing Fractions

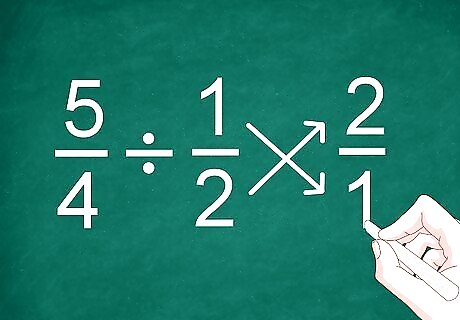
Invert the second fraction. The simplest way to divide fractions, even those with unlike denominators, is to flip the second fraction before you calculate the sum. For example, with 5/4 ÷ 1/2 you should flip the 1/2 fraction so it appears as 2/1.

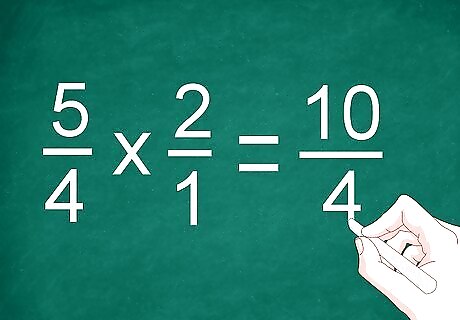
Multiply the numerators and denominators. Multiply the fractions straight across to multiply the numerators. Put the result over a dividing line and multiply the denominators. Put the result under the dividing line. To continue the example, you'd multiply 5/4 by 2/1 to get 10/4.

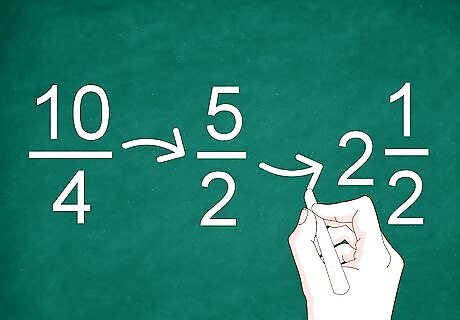
Simplify the results, if needed. If your answer is an improper fraction or can be reduced, simplify the fraction. Use the greatest common factor to reduce the fraction. For example, the greatest common factor for 10/4 is 2 so your simplified answer is 5/2. Since this is an improper fraction, turn it into a whole number with a fraction. 5/2 becomes 2 1/2.