views
Starting with the Basics
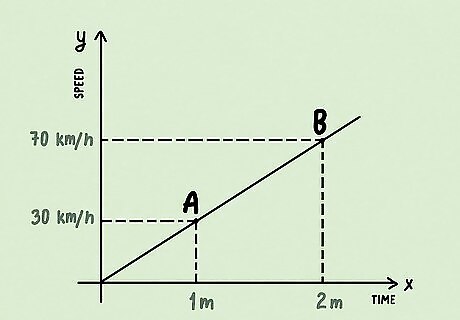
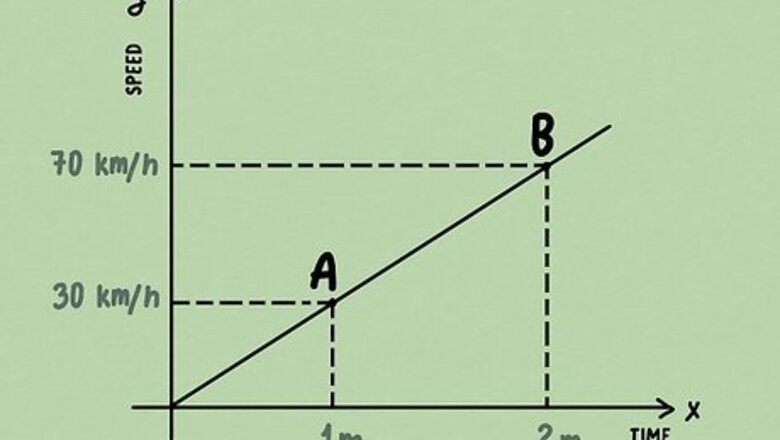
Know that a derivative is a calculation of the rate of change of a function. For instance, if you have a function that describes how fast a car is going from point A to point B, its derivative will tell you the car's acceleration from point A to point B—how fast or slow the speed of the car changes.
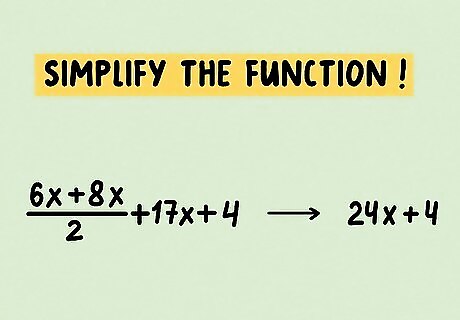
Simplify the function. Functions that are not simplified will still yield the same derivative, but it can be much more difficult to calculate. Example equation to simplify: (6x + 8x)/2 +17x +4 (14x)/2 + 17x + 4 7x + 17x + 4 24x + 4

Identify the form of the function. Learn the various forms. Just a number (e.g., 4) A number multiplied by a variable with no exponent (e.g., 4x) A number multiplied by a variable with an exponent (e.g., 4x^2) Addition (e.g., 4x + 4) Multiplication of variables (e.g., of the form x*x) Division of variables (e.g., of the form x/x)
Finding the Derivates of Different Forms
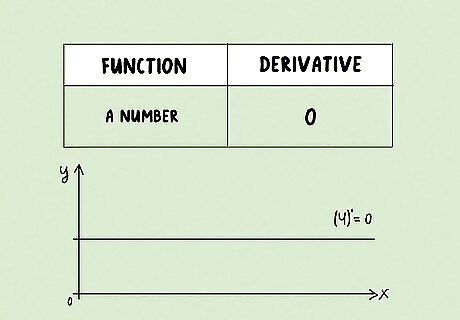
A number: The derivative of a function of this form is always zero. This is because there is no change in the function—the value of the function will always be the number that you're given. Here are some examples: (4)' = 0 (-234059)' = 0 (pi)' = 0
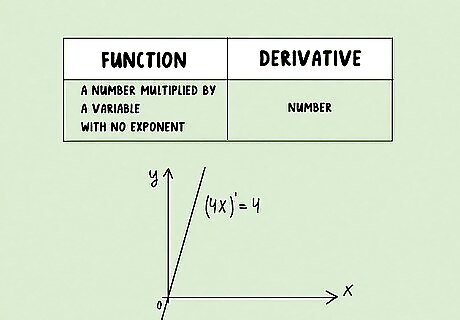
A number multiplied by a variable with no exponent: The derivative of a function of this form is always the number. If x does not have an exponent, the function is growing at a constant, steady, unchanging rate. You may recognize this trick from the linear equation y = mx + b. Check out these examples: (4x)' = 4 (x)' = 1 (-23x)' = -23
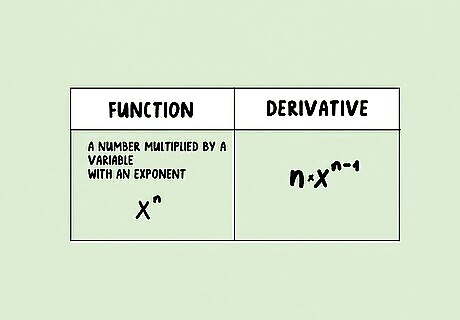
A number multiplied by a variable with an exponent: Subtract one from the exponent. Multiply the number by the value of the exponent. For instance: (4x^3)' = (4*3)(x^(3-1)) = 12x^2 (2x^7)' = 14x^6 (3x^(-1))' = -3x^(-2)
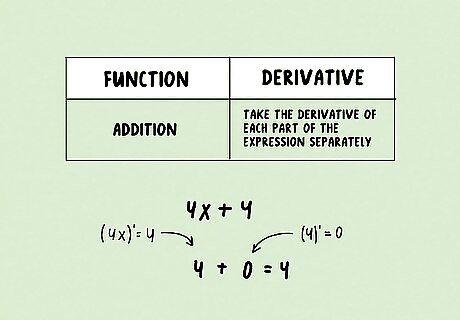
Addition: Take the derivative of each part of the expression separately. For example: (4x + 4)' = 4 + 0 = 4 ((x^2) + 7x)' = 2x + 7

Multiplication of variables: Multiply the first variable by the derivative of the second variable. Multiply the second variable by the derivative of the first variable. Add your two results together. Here's an example: ((x^2)*x)' = (x^2)*1 + x*2x = (x^2) + 2x*x = 3x^2

Division of variables: Multiply the bottom variable by the derivative of the top variable. Multiply the top variable by the derivative of the bottom variable. Subtract your result in Step 2 from your result in Step 1. Be careful, order matters! Divide your result in Step 3 with the square of the bottom variable. Check out this example: ((x^7)/x)' = (7x^6*x – 1*x^7)/(x^2) = (7x^7 - x^7)/(x^2) = 6x^7/x^2 = 6x^5 This is perhaps the hardest of the tricks to do, but it's well worth the effort. Make sure to do the steps in order and subtract in the correct order, and this will go smoothly.















Comments
0 comment